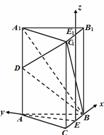
题目内容
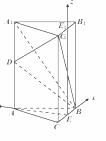
如图,在正三棱柱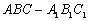 中,已知
中,已知 ,
,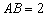 ,
,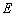 是
是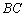 的中点,
的中点, 在棱
在棱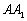 上.
上.
(I)求异面直线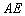 与
与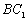 所成角;
所成角;
(II)若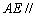 平面
平面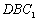 ,求
,求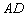 长;
长;
(III)在棱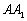 上是否存在点
上是否存在点 ,使得二面角
,使得二面角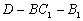 的大小等于
的大小等于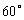 ,若存在,求
,若存在,求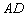 的长;若不存在,说明理由.
的长;若不存在,说明理由.
解:方法1:(I)取 中点
中点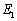 ,建立如图所示坐标系,
,建立如图所示坐标系,
则 ,
, ,
,
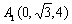 ,
, ,
, ,设
,设 ,
,
∴ ,
, ,
, ,
,
∵ ,∴异面直线
,∴异面直线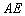 与
与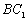 所成角是
所成角是 ;
;
(II)设 是面
是面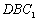 的法向量,则
的法向量,则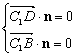 ,得
,得 ,
,
∵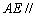 平面
平面 ,∴
,∴ ,∴
,∴ ,即
,即 ;
;
(III)∵ 是平面
是平面 的法向量,
的法向量,
∴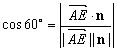 ,即
,即 ,解得
,解得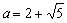 ,
,
∵点 在棱
在棱 上,∴
上,∴ ,而
,而 ,∴在棱
,∴在棱 上的点
上的点 是不存在的.
是不存在的.
 方法2:(I)∵
方法2:(I)∵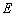 是
是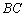 的中点,∴
的中点,∴ 面
面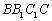 ,
,
∴
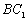 ,异面直线
,异面直线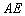 与
与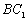 所成角是
所成角是 ;
;
(II)取 中点
中点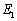 ,建立如图所示坐标系,
,建立如图所示坐标系,
则 ,
, ,
,
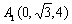 ,
, ,
, ,设
,设 ,
,
∴ ,
, ,
, ,
,
∵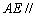 平面
平面 ,∴存在唯一的
,∴存在唯一的 使得
使得 ,
,
∴ ,∴
,∴ ,即
,即 ;
;
(III)设 是面
是面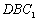 的法向量,则
的法向量,则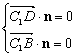 ,得
,得 ,
,
∵ 是平面
是平面 的法向量,
的法向量,
∴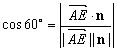 ,即
,即 ,解得
,解得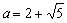 ,
,
∵ 点 在棱
在棱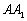 上,∴
上,∴ ,而
,而 ,∴ 在棱
,∴ 在棱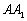 上的点
上的点 是不存在的.
是不存在的.

练习册系列答案
相关题目
 满足
满足 ,使
,使 取得最大值的最优解有两个,则
取得最大值的最优解有两个,则 的最小值为
的最小值为 C、1 D、
C、1 D、
 的导数为 。
的导数为 。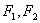 ,若曲线C上存在点P满足
,若曲线C上存在点P满足 :
: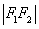 :
: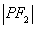 = 4:3:2,则曲线C的离心率等于 ( )
= 4:3:2,则曲线C的离心率等于 ( ) B.
B. 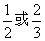 C.
C.  D.
D. 
 为两个定点,
为两个定点,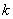 为非零常数,
为非零常数,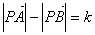 ,则动点
,则动点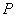 的轨迹为双曲线;
的轨迹为双曲线;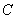 上一定点
上一定点 和一动点
和一动点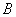 ,
,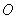 为坐标原点,若
为坐标原点,若 则动点
则动点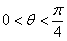 ,则双曲线
,则双曲线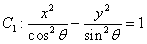 与
与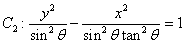 的离心率相同;
的离心率相同;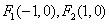 和一动点
和一动点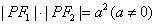 ,则点
,则点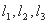 是空间三条不同的直线,则下列命题正确的是( )
是空间三条不同的直线,则下列命题正确的是( )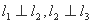
 B.
B.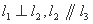
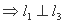

 共面 D.
共面 D. 共点
共点 上任一点连线的中点的轨迹方程是( )
上任一点连线的中点的轨迹方程是( ) B.
B.
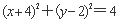 D.
D.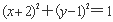
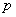 :“
:“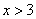 ”是“
”是“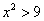 ”的充要条件,命题
”的充要条件,命题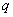 :“
:“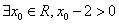 ”的否定是“
”的否定是“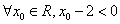 ”
”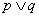 ”为真 B.“
”为真 B.“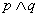 ”为真 C.
”为真 C.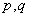 均为假
均为假