题目内容
(本小题满分14分)
在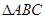 中,角A,B,C的对边分别为a,b,c,且
中,角A,B,C的对边分别为a,b,c,且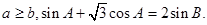
(1)求角C的大小;
(2)求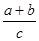 的最大值.
的最大值.
(1)A+B= ,C=
,C= .(2)A=
.(2)A= 时,
时, 取最大值2.
取最大值2.
解析试题分析:(1)sinA+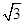 cosA=2sinB即2sin(A+
cosA=2sinB即2sin(A+ )=2sinB,则sin(A+
)=2sinB,则sin(A+ )=sinB.
)=sinB.
因为0<A,B<p,又a≥b进而A≥B,
所以A+ =p-B,故A+B=
=p-B,故A+B= ,C=
,C= .
.
(2)由正弦定理及(Ⅰ)得 =
= =
= [sinA+sin(A+
[sinA+sin(A+ )]=
)]=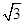 sinA+cosA=2sin(A+
sinA+cosA=2sin(A+ ).
).
当A= 时,
时, 取最大值2.
取最大值2.
考点:本题主要考查三角函数恒等变换,正弦定理的应用。
点评:典型题,为研究三角函数的图象和性质,往往需要将函数“化一”。本题由正弦定理建立了 的表达式,通过“化一”,利用三角函数性质,求得最大值。
的表达式,通过“化一”,利用三角函数性质,求得最大值。

练习册系列答案
相关题目
 顶点的分别为
顶点的分别为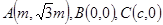 ,其中
,其中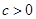 .
.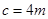 ,求
,求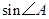 的值;
的值;
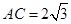 ,求
,求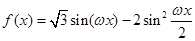 (
(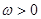 )的最小正周期为
)的最小正周期为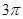 ,
,  时,求函数
时,求函数 的最小值;
的最小值;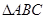 中,若
中,若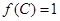 ,且
,且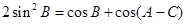 ,求
,求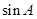 的值。
的值。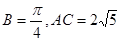 ,
,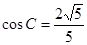 .
.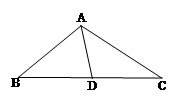
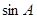 ;
;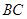 的中点为
的中点为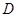 ,求中线
,求中线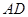 的长.
的长. 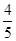 .
.
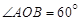 ,
,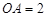 ,
,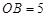 ,在线段
,在线段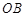 上任取一点
上任取一点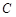 ,
,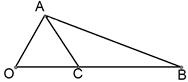
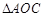 为钝角三角形的概率;
为钝角三角形的概率;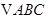 的内角
的内角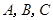 的对边分别是
的对边分别是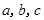 ,且
,且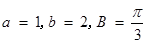 .
.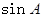 的值; (2) 求
的值; (2) 求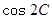 的值.
的值.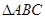 外接圆的半径为2,
外接圆的半径为2,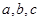 分别是
分别是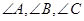 的对边
的对边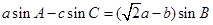
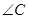 (2)求
(2)求