题目内容
已知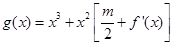 ,
, ,
, .
.
(1)当 时,试比较
时,试比较 与
与 的大小关系;
的大小关系;
(2)猜想 与
与 的大小关系,并给出证明.
的大小关系,并给出证明.
(1) ,
, ,
, ,(2)
,(2)
解析试题分析:(1)归纳过程,代入验证即可. 当 时,
时, ,
, ,所以
,所以 ;当
;当 时,
时, ,
, ,所以
,所以 ;当
;当 时,
时, ,
, ,所以
,所以 .(2)由(1),猜想
.(2)由(1),猜想 ,用数学归纳法给出证明时注意格式完整,推导有理.本题推导应用作差法证明不等式.假设当
,用数学归纳法给出证明时注意格式完整,推导有理.本题推导应用作差法证明不等式.假设当 时不等式成立,即
时不等式成立,即 ,那么,当
,那么,当 时,
时, ,因为
,因为 所以
所以 .
.
(1)当 时,
时, ,
, ,所以
,所以 ; 1分
; 1分
当 时,
时, ,
, ,所以
,所以 ; 2分
; 2分
当 时,
时, ,
, ,所以
,所以 . 4分
. 4分
(2)由(1),猜想 ,下面用数学归纳法给出证明: 6分
,下面用数学归纳法给出证明: 6分
①当 时,不等式显然成立. 7分
时,不等式显然成立. 7分
②假设当 时不等式成立,即
时不等式成立,即 ,...9分
,...9分
那么,当 时,
时, , 11分
, 11分
因为 ,14分
,14分
所以 . 15分
. 15分
由①、②可知,对一切 ,都有
,都有 成立. 16分
成立. 16分
考点:归纳猜想证明

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 个等式:
个等式:




 个等式,并猜想第
个等式,并猜想第 个等式;
个等式;
 ,(其中
,(其中 )
) 及
及 ;
; 与
与 的大小,并说明理由.
的大小,并说明理由. ,求证:
,求证: ;
;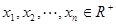 ,且
,且 ,
, .
. 的展开式中,
的展开式中, 的系数为
的系数为 ,
, 的系数为
的系数为 ,其中
,其中
 ,对
,对 恒成立?证明你的结论.
恒成立?证明你的结论. 是函数
是函数
 的零点.
的零点. ;
;
 .
.