题目内容
观察以下
个等式：
照以上式子规律：
写出第
个等式，并猜想第
个等式；
用数学归纳法证明上述所猜想的第个等式成立．
（1）
;（2）
解析试题分析：（1）根据题目给我们的几个式子易得出结论；（2）先猜想第n个式子为
，当n=1,n=k时的式子成立，然后利用规纳总结
也成立，即可证明．
试题解析：（1）第6个等式为 2分
（2）猜想：第个等式为
4分
下面用数学归纳法给予证明：
①当
时，由已知得原式成立； 5分
②假设当
时，原式成立，
即
6分
那么，当时，
故时，原式也成立 11分
由①②知，
成立 13分
考点：1，学生对规律的把握2，学生对规纳总结方法的应用．
练习册系列答案
相关题目
，空间任意三条两两平行且不共面的直线
，若直线
与
，
，
，则平面
为三角形
的三边，求证：
，
，
．
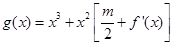时，试比较
与
的大小关系；
与
的大小关系，并给出证明．
，则三角形面积
.根据类比推理，在空间中，如果四面体内切球的半径为R，其四个面的面积分别为
,则四面体的体积V=_ __.
，
,
，
，则第5个等式为 ，…,推广到第
个等式为__ _；（注意：按规律写出等式的形式，不要求计算结果．）