题目内容
(1)已知 ,求证:
,求证: ;
;
(2)已知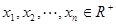 ,且
,且 ,
,
求证: .
.
证明见解析.
解析试题分析:(1)本题证明只要利用作差法即可证得;(2)这个不等式比较复杂,考虑到不等式的形式,我们可用数学归纳法证明,关键在 时的命题如何应用
时的命题如何应用 时的结论,
时的结论, 中要把两个括号合并成一个,又能应用
中要把两个括号合并成一个,又能应用 时的结论证明
时的结论证明 时的结论,当
时的结论,当 时,结论已经成立,当
时,结论已经成立,当 时,在
时,在 中可找到一个,不妨设为
中可找到一个,不妨设为 ,使
,使 ,即
,即 ,从而有
,从而有


 ,这样代入进去可证得
,这样代入进去可证得 时结论成立.
时结论成立.
(1)因为 ,所以
,所以 ,即
,即 ; 2分
; 2分
(2)证法一(数学归纳法):(ⅰ)当 时,
时, ,不等式成立. 4分
,不等式成立. 4分
(ⅱ)假设 时不等式成立,即
时不等式成立,即 成立. 5分
成立. 5分
则 时,若
时,若 ,则命题成立;若
,则命题成立;若 ,则
,则 中必存在一个数小于1,不妨设这个数为
中必存在一个数小于1,不妨设这个数为 ,从而
,从而 ,即
,即 .
. 同理可得,
同理可得,
所以





故 时,不等式也成立. 9分
时,不等式也成立. 9分
由(ⅰ)(ⅱ)及数学归纳法原理知原不等式成立. 10分
证法二:(恒等展开)左右展开,得
 由平均值不等式,得
由平均值不等式,得
 8分
8分
故

 . 10分
. 10分
考点:(1)比较法证不等式;(2)数学归纳法证不等式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
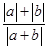 ≤
≤ .
.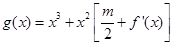 ,
, ,
, .
. 时,试比较
时,试比较 与
与 的大小关系;
的大小关系; 与
与 的大小关系,并给出证明.
的大小关系,并给出证明. 中,已知
中,已知 ,
, ,
, (
( ,
, ).
). ,
,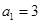 时,分别求
时,分别求 的值,判断
的值,判断 是否为定值,并给出证明;
是否为定值,并给出证明; ,使得
,使得 为完全平方数.
为完全平方数. 计算
计算 由此推测出
由此推测出 的计算公式,并用数学归纳法证明.
的计算公式,并用数学归纳法证明. (其中a>0且a≠1).记Sn是数列{an}的前n项和,试比较Sn与
(其中a>0且a≠1).记Sn是数列{an}的前n项和,试比较Sn与 logabn+1的大小,并证明你的结论.
logabn+1的大小,并证明你的结论.
 的值.
的值. 没有最小数”时,可用反证法证明.
没有最小数”时,可用反证法证明. 是
是 中的最小数,则取
中的最小数,则取 ,可得:
,可得: ,与假设中“
,与假设中“ 是
是 没有最大数”,也可以用反证法证明.我们可以假设
没有最大数”,也可以用反证法证明.我们可以假设 是
是 中的最大数,则可以找到
中的最大数,则可以找到 ▲ (用
▲ (用 ,
, 表示),由此可知
表示),由此可知 ,
, ,这与假设矛盾!所以数集
,这与假设矛盾!所以数集