题目内容
如图，正方形OABC的顶点O在坐标原点，其中点A（-3，4），AB边与y轴交与点D．（1）求直线AB解析式；
（2）求△AOD的面积及其外接圆的面积；
（3）问△AOD的外接圆与BC所在的直线是否相切？
考点：直线和圆的方程的应用
专题：综合题,直线与圆
分析：（1）求出直线AB的斜率，即可求直线AB解析式；
（2）求出圆心D的坐标，即可求△AOD的面积及其外接圆的面积；
（3）求出BC的方程，判断圆心到BC的距离与半径的关系，即可判断△AOD的外接圆与BC所在的直线是否相切
（2）求出圆心D的坐标，即可求△AOD的面积及其外接圆的面积；
（3）求出BC的方程，判断圆心到BC的距离与半径的关系，即可判断△AOD的外接圆与BC所在的直线是否相切
解答：
解：（1）∵点A（-3，4），
∴kOA=-
，
∴kAB=
，
∴直线AB解析式为y-4=
（x+3），即3x-4y+25=0；
（2）由（1）知D（0，
），
∴△AOD的面积S=
•
•3=
，
∵△AOD的外接圆的半径为
∴△AOD的外接圆的面积为π•(
)2=
；
（3）∵OA的方程为4x+3y=0，
∴设BC的方程为4x+3y+c=0，
∵AB=5，
∴
=5，
∴c=±25，
由图形知，BC的方程为4x+3y+25=0
∵△AOD的外接圆的圆心为（0，
）
∴圆心到BC的距离为
=
＞
∴△AOD的外接圆与BC所在的直线相离．
∴kOA=-
| 4 |
| 3 |
∴kAB=
| 3 |
| 4 |
∴直线AB解析式为y-4=
| 3 |
| 4 |
（2）由（1）知D（0，
| 25 |
| 4 |
∴△AOD的面积S=
| 1 |
| 2 |
| 25 |
| 4 |
| 75 |
| 8 |
∵△AOD的外接圆的半径为
| 25 |
| 8 |
∴△AOD的外接圆的面积为π•(
| 25 |
| 8 |
| 625π |
| 64 |
（3）∵OA的方程为4x+3y=0，
∴设BC的方程为4x+3y+c=0，
∵AB=5，
∴
| |c| | ||
|
∴c=±25，
由图形知，BC的方程为4x+3y+25=0
∵△AOD的外接圆的圆心为（0，
| 25 |
| 8 |
∴圆心到BC的距离为
|3•
| ||
| 5 |
| 55 |
| 8 |
| 25 |
| 8 |
∴△AOD的外接圆与BC所在的直线相离．
点评：本题考查直线与圆的方程，考查直线与圆的位置关系，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
若两个非零向量
，
满足|
+
|=|
-
|=2|
|，则向量
+
与
-
的夹角为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
由a1=1，an+1=
给出的数列{an}的第33项是（ ）
| an |
| 3an+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
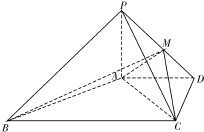如图四棱锥P-ABCD中，PA⊥平面ABCD，AD∥BC，ADCD，且AD=CD=2
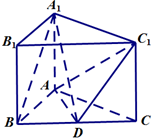如图三棱柱ABC-A1B1C1中，侧棱与底面垂直，△ABC是等边三角形，点D是BC的中点．