题目内容
(本小题满分12分)设函数f(x)=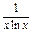 (x>0且x≠1).
(x>0且x≠1).
(1)求函数f(x)的单调区间;
(2)已知2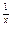 >xa对任意x∈(0,1)成立,求实数a的取值范围.
>xa对任意x∈(0,1)成立,求实数a的取值范围.
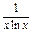 (x>0且x≠1).
(x>0且x≠1).(1)求函数f(x)的单调区间;
(2)已知2
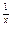 >xa对任意x∈(0,1)成立,求实数a的取值范围.
>xa对任意x∈(0,1)成立,求实数a的取值范围.解:(1)f′(x)=-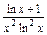 ,若f′(x)=0,则x=
,若f′(x)=0,则x= .
.
列表如下:
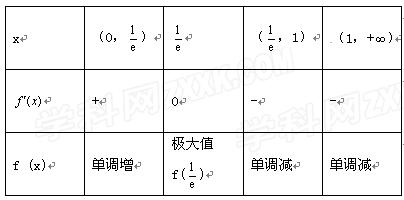
所以f(x)的单调增区间为(0, ),
),
单调减区间为( ,1)和(1,+∞).
,1)和(1,+∞).
(2)在2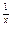 >xa两边取对数,得
>xa两边取对数,得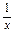 ln2>alnx.
ln2>alnx.
由于x∈(0,1),所以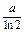 >
>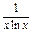 . ①
. ①
由(1)的结果知,
当x∈(0,1)时,f(x)≤f( )=-e.
)=-e.
为使①式对所有x∈(0,1)成立,当且仅当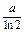 >-e,
>-e,
即a>-eln2.
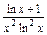 ,若f′(x)=0,则x=
,若f′(x)=0,则x= .
.列表如下:

所以f(x)的单调增区间为(0,
 ),
),单调减区间为(
 ,1)和(1,+∞).
,1)和(1,+∞).(2)在2
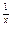 >xa两边取对数,得
>xa两边取对数,得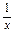 ln2>alnx.
ln2>alnx.由于x∈(0,1),所以
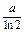 >
>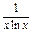 . ①
. ①由(1)的结果知,
当x∈(0,1)时,f(x)≤f(
 )=-e.
)=-e.为使①式对所有x∈(0,1)成立,当且仅当
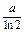 >-e,
>-e,即a>-eln2.
略

练习册系列答案
相关题目
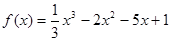 的极大值是
的极大值是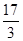
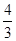

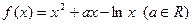 .
.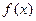 在
在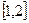 上是减函数,求实数
上是减函数,求实数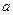 的取值范围;
的取值范围;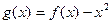 ,是否存在实数
,是否存在实数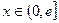 时,函数
时,函数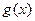 的最小值是
的最小值是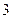 ,若存在,求出实数
,若存在,求出实数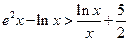 .
.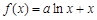 在区间
在区间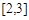 上单调递增,则实数a的取值范围为( ).
上单调递增,则实数a的取值范围为( ).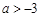
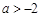
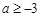
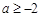
 ,则
,则 等于
等于 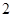


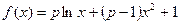 .
.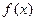 的单调性;
的单调性;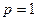 时,
时,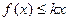 恒成立,求实数
恒成立,求实数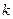 的取值范围;
的取值范围;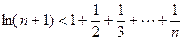
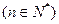 .
. )已知函数
)已知函数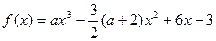 (a为常数)
(a为常数)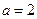 时,分析函数
时,分析函数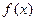 的单调性;
的单调性;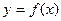 与
与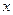 轴的公共点的个数。
轴的公共点的个数。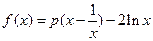 ,
,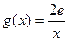 ,
,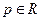 ,
,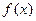 在
在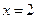 处取得极值,求
处取得极值,求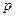 的值;
的值;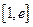 上至少存在一点
上至少存在一点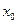 ,使得
,使得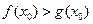 成立,求
成立,求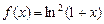
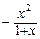 .
.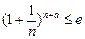 对任意的
对任意的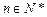 都成立(其中e是自然对数的底数),求a的最大值。
都成立(其中e是自然对数的底数),求a的最大值。