题目内容
函数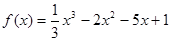 的极大值是
的极大值是
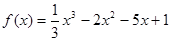 的极大值是
的极大值是A.-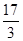 | B.1 | C.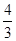 | D. |
D
分析:由f(x)=  x3-2x2-5x+1,令f′(x)=x2-4x-5=0,得x=-1,或x=5,列表讨论,能求出函数f(x)=
x3-2x2-5x+1,令f′(x)=x2-4x-5=0,得x=-1,或x=5,列表讨论,能求出函数f(x)=  x3-2x2-5x+1的极大值.
x3-2x2-5x+1的极大值.
解:∵f(x)= x3-2x2-5x+1,
x3-2x2-5x+1,
∴f′(x)=x2-4x-5,
令f′(x)=x2-4x-5=0,得x=-1,或x=5,
列表讨论,得
∴f(x)= x3-2x2-5x+1在x=-1处取极大值:
x3-2x2-5x+1在x=-1处取极大值:
f(-1)=- -2+5+1=
-2+5+1= ,
,
故选D.
 x3-2x2-5x+1,令f′(x)=x2-4x-5=0,得x=-1,或x=5,列表讨论,能求出函数f(x)=
x3-2x2-5x+1,令f′(x)=x2-4x-5=0,得x=-1,或x=5,列表讨论,能求出函数f(x)=  x3-2x2-5x+1的极大值.
x3-2x2-5x+1的极大值.解:∵f(x)=
 x3-2x2-5x+1,
x3-2x2-5x+1,∴f′(x)=x2-4x-5,
令f′(x)=x2-4x-5=0,得x=-1,或x=5,
列表讨论,得
| x | (-∞,-1) | -1 | (-1,5) | 5 | (5,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| | ↑ | 极大值 | ↓ | 极小值 | ↑ |
 x3-2x2-5x+1在x=-1处取极大值:
x3-2x2-5x+1在x=-1处取极大值:f(-1)=-
 -2+5+1=
-2+5+1= ,
,故选D.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
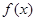 在
在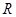 上可导,则
上可导,则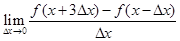 等于( )
等于( )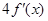
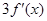
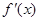
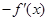
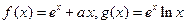 (
(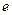 是自然对数的底数).
是自然对数的底数).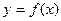 在
在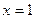 处的切线也是抛物线
处的切线也是抛物线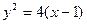 的切线,求
的切线,求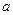 的值;
的值;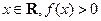 恒成立,试确定实数
恒成立,试确定实数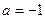 时,是否存在
时,是否存在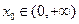 ,使曲线
,使曲线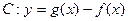 在点
在点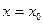 处的切线斜率与
处的切线斜率与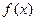 在
在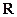 上的最小值相等?若存在,求符合条件的
上的最小值相等?若存在,求符合条件的 的个数;若不存在,请说明理由.
的个数;若不存在,请说明理由.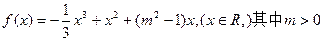
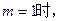 曲线
曲线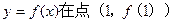 处的切线斜率
处的切线斜率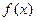 有三个互不相同的零点0,
有三个互不相同的零点0,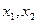 ,且
,且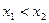 .若对任意的
.若对任意的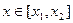 ,
,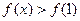 恒成立,求m的取值范围.
恒成立,求m的取值范围.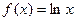
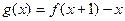 的最大值;
的最大值;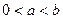 时,求证
时,求证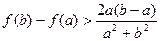 ;
;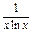 (x>0且x≠1).
(x>0且x≠1).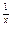 >xa对任意x∈(0,1)成立,求实数a的取值范围.
>xa对任意x∈(0,1)成立,求实数a的取值范围.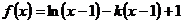
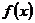 的单调区间和最大值;
的单调区间和最大值;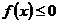 恒成立,求
恒成立,求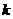 的取值范围;
的取值范围;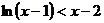 在
在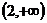 上恒成立;
上恒成立;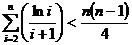
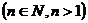
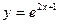 与
与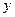 轴的交点的切线方程为_______________。
轴的交点的切线方程为_______________。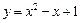 在点(1,0)处的切线方程为 ;
在点(1,0)处的切线方程为 ;