题目内容
函数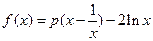 ,
,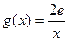 ,
,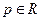 ,
,
(1)若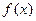 在
在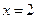 处取得极值,求
处取得极值,求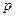 的值;
的值;
(2)若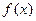 在其定义域内为单调函数,求
在其定义域内为单调函数,求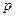 的取值范围;
的取值范围;
(3)若在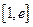 上至少存在一点
上至少存在一点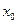 ,使得
,使得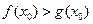 成立,求
成立,求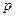 的取值范围.
的取值范围.
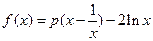 ,
,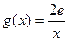 ,
,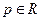 ,
,(1)若
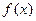 在
在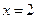 处取得极值,求
处取得极值,求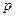 的值;
的值;(2)若
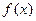 在其定义域内为单调函数,求
在其定义域内为单调函数,求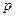 的取值范围;
的取值范围;(3)若在
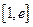 上至少存在一点
上至少存在一点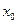 ,使得
,使得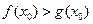 成立,求
成立,求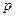 的取值范围.
的取值范围.解: (1)
(1)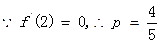 .
.
(2)由已知,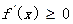 恒成立,或
恒成立,或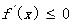 恒成立.
恒成立.
若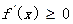 恒成立,即
恒成立,即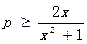 在
在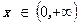 恒成立,即
恒成立,即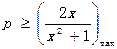
若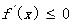 恒成立,即
恒成立,即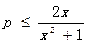 在
在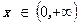 恒成立,即
恒成立,即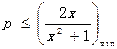
令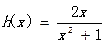
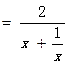 ,则当
,则当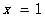 时,
时,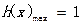 ;当
;当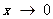 或
或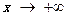 时,
时,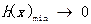
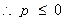 或
或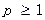
(3)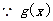 在
在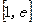 上单调递减,
上单调递减,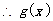 的值域为
的值域为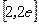 .
.
①若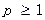 ,由(2)知:
,由(2)知: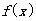 在
在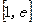 上单调递增,
上单调递增,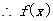 的值域为
的值域为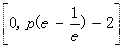 .
.
要满足题意,则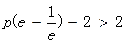 即可,
即可,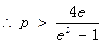
②若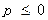 ,由(2)知:
,由(2)知: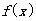 在
在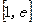 上单调递减,的值域为
上单调递减,的值域为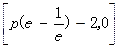
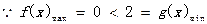 ,
,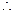 此时不满足题
此时不满足题 意.
意.
③若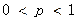 时,
时,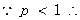
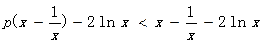
由(2)知:当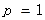 时,
时,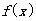 在
在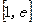 上单调递增,
上单调递增, 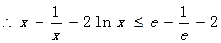 又
又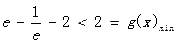 ,
,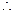 此时不满足题意.综上所述,
此时不满足题意.综上所述,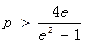 .
.
 (1)
(1)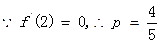 .
.(2)由已知,
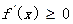 恒成立,或
恒成立,或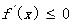 恒成立.
恒成立.若
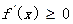 恒成立,即
恒成立,即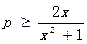 在
在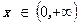 恒成立,即
恒成立,即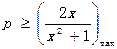
若
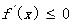 恒成立,即
恒成立,即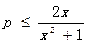 在
在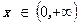 恒成立,即
恒成立,即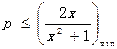
令
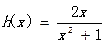
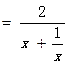 ,则当
,则当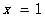 时,
时,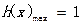 ;当
;当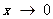 或
或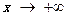 时,
时,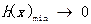
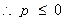 或
或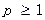
(3)
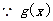 在
在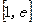 上单调递减,
上单调递减,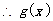 的值域为
的值域为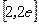 .
.①若
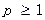 ,由(2)知:
,由(2)知: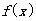 在
在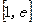 上单调递增,
上单调递增,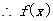 的值域为
的值域为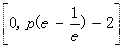 .
.要满足题意,则
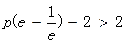 即可,
即可,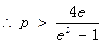
②若
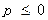 ,由(2)知:
,由(2)知: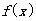 在
在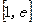 上单调递减,的值域为
上单调递减,的值域为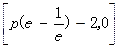
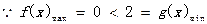 ,
,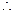 此时不满足题
此时不满足题 意.
意.③若
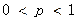 时,
时,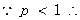
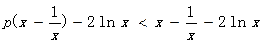
由(2)知:当
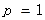 时,
时,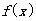 在
在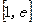 上单调递增,
上单调递增, 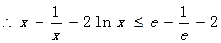 又
又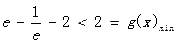 ,
, 此时不满足题意.综上所述,
此时不满足题意.综上所述,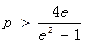 .
.略

练习册系列答案
相关题目
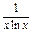 (x>0且x≠1).
(x>0且x≠1).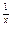 >xa对任意x∈(0,1)成立,求实数a的取值范围.
>xa对任意x∈(0,1)成立,求实数a的取值范围.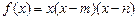 .
.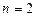 时,若函数
时,若函数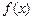 在
在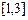 上单调递减,求实数
上单调递减,求实数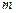 的取值范围;
的取值范围;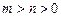 ,
,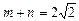 ,且过原点存在两条互相垂直的直线与曲线
,且过原点存在两条互相垂直的直线与曲线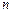 的值.
的值.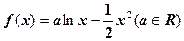 。(1)讨论函数
。(1)讨论函数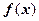 的单调性;(2)当
的单调性;(2)当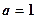 时,设
时,设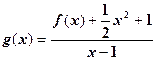 ,若
,若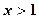 时,
时,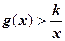 恒成立。求整数
恒成立。求整数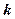 的最大值。
的最大值。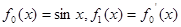 ,
,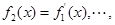
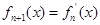 ,n∈N,则
,n∈N,则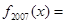 ( )
( )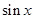
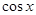
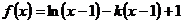
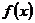 的单调区间和最大值;
的单调区间和最大值;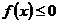 恒成立,求
恒成立,求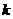 的取值范围;
的取值范围;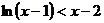 在
在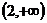 上恒成立;
上恒成立;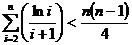
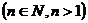
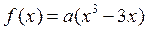 的递减区间为(-1,1),则a的取值范围是 .
的递减区间为(-1,1),则a的取值范围是 .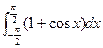 =__________________________.
=__________________________.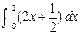 = .
= .