题目内容

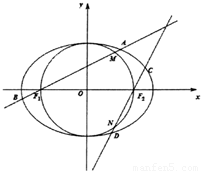
如图，F₁和F₂分别是双曲线 $数学公式$ 的两个焦点，A和B是以O为圆心，以|OF₁|为半径的圆与该双曲线左支的两个交点，且△F₂AB是等边三角形，则双曲线的半焦距c=________．

$\text{[math]}$
分析：连接AF₁，根据△F₂AB是等边三角形可知∠AF₂B=60°，根据F₁F₂是圆的直径可表示出|AF₁|、|AF₂|，再由双曲线的定义可得 $\text{[math]}$ c-c=2a，即可得到离心率的值．
解答：连接AF₁，则∠F₁AF₂=90°，∠AF₂B=60°
∴|AF₁|= $\text{[math]}$ ，
|AF₂|= $\text{[math]}$ |F₁F₂|= $\text{[math]}$ c，
∴ $\text{[math]}$ c-c=2a，
∴e= $\text{[math]}$ =1+ $\text{[math]}$ ，
又a= $\text{[math]}$ ，
∴c= $\text{[math]}$ （1+ $\text{[math]}$ ）= $\text{[math]}$
故答案为： $\text{[math]}$ ．
点评：本题主要考查直线与圆锥曲线的综合问题、双曲线的基本性质--离心率的求法．考查基础知识的灵活应用．

练习册系列答案

阶梯训练系列答案

王朝霞小升初重点校系列答案

专项卷和真题卷系列答案

文曲星中考总复习系列答案

问题引领系列答案

先锋题典系列答案

知识大集结系列答案

随堂口算系列答案

小学升学夺冠系列答案

培优好题系列答案

相关题目

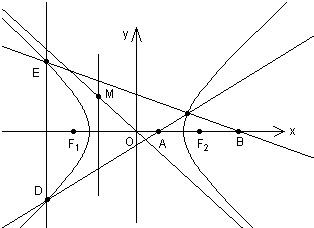如图，双曲线

=1（a＞0，b＞0）的离心率为

，F1、F₂分别为左、右焦点，M为左准线与渐近线在第二象限内的交点，且

．
（I）求双曲线的方程；
（II）设A（m，0）和B(

，0)（0＜m＜1）是x轴上的两点．过点A作斜率不为0的直线l，使得l交双曲线于C、D两点，作直线BC交双曲线于另一点E．证明直线DE垂直于x轴．中心O为圆心，分别以a和b为半径作大圆和．

（2012•温州二模）如图，F₁，F₂是椭圆

+y²=1的左、右焦点，M，N是以F₁F₂为直径的圆上关于X轴对称的两个动点．
（I）设直线MF₁、NF₂的斜率分别为k₁，k₂，求k₁•k₂值；
（II）直线MF₁和NF₂与椭圆的交点分别为A，B和C、D．问是若存在实数λ，使得λ（|AB|+|CD|）=|AB|•|CD|恒成立．若存在，求实数λ的值．若不存在，请说明理由．

（本小题满分14分）

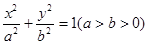如图，F₁、F₂分别是椭圆的左右焦点，M为椭圆上一点，MF₂垂直于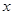轴，椭圆下顶点和右顶点分别为A，B，且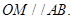

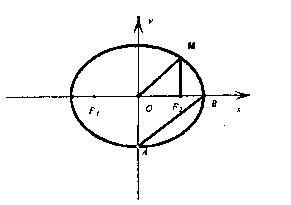
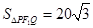（1）求椭圆的离心率；

（2）过F₂作OM垂直的直线交椭圆于点P，Q，若，求椭圆方程。

如图，F₁，F₂分别是椭圆

（a＞b＞0）的左、右焦点，M为椭圆上一点，MF₂垂直于x轴，椭圆下顶点和右顶点分别为A、B，且OM∥AB，
（1）求椭圆的离心率；
（2）过F₂作于OM垂直的直线交椭圆于点P、Q，若

，求椭圆的方程。

如图，F₁，F₂是椭圆

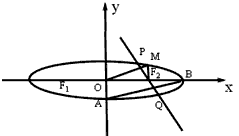
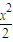+y²=1的左、右焦点，M，N是以F₁F₂为直径的圆上关于X轴对称的两个动点．
（I）设直线MF₁、NF₂的斜率分别为k₁，k₂，求k₁•k₂值；
（II）直线MF₁和NF₂与椭圆的交点分别为A，B和C、D．问是若存在实数λ，使得λ（|AB|+|CD|）=|AB|•|CD|恒成立．若存在，求实数λ的值．若不存在，请说明理由．