题目内容
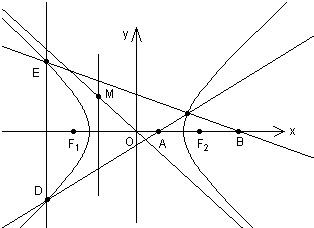 如图,双曲线
如图,双曲线| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| F1M |
| F2M |
| 1 |
| 4 |
(I)求双曲线的方程;
(II)设A(m,0)和B(
| 1 |
| m |
分析:(I)设点M(x,y),根据题设条件联立方程求得M的坐标,根据
.
=-
.求得a,b和c的关系利用a2+b2=c2求得c,b和a,答案可得.
(II)设点C(x1,y1),D(x2,y2),E(x3,y3),则可表示出直线l的方程,直线与双曲线联立方程,可求得x1x2的表达式,求得x2的表达式,同理可求得x3的表达式,最后得出以x2=x3,判断出故直线DE垂直于x轴.
| F1M |
| F2M |
| 1 |
| 4 |
(II)设点C(x1,y1),D(x2,y2),E(x3,y3),则可表示出直线l的方程,直线与双曲线联立方程,可求得x1x2的表达式,求得x2的表达式,同理可求得x3的表达式,最后得出以x2=x3,判断出故直线DE垂直于x轴.
解答:(I)解:根据题设条件,F1(-c,0),F2(c,0).
设点M(x,y),则x、y满足
因e=
=
,解得M(-
,
),
故
.
=(-
+c,
).(-
-c,
)=
a2-c2+
b2=-
.
利用a2+b2=c2,得c2=
,于是a2=1,b2=
.
因此,所求双曲线方程为x2-4y2=1.
(II)解:设点C(x1,y1),D(x2,y2),E(x3,y3),则直线l的方程为y=
(x-m).
于是C(x1,y1)、D(x2,y2)两点坐标满足
将①代入②得(x12-2x1m+m2-4y12)x2+8my12x-4y12m2-x12+2mx1-m2=0.
由已知,显然m2-2x1m+1≠0.于是x1x2=-
.
因为x1≠0,得x2=-
.
同理,C(x1,y1)、E(x3,y3)两点坐标满足
可解得x3=-
=-
.
所以x2=x3,故直线DE垂直于x轴.
设点M(x,y),则x、y满足
|
因e=
| c |
| a |
| ||
| 2 |
| 2a | ||
|
| 2b | ||
|
故
| F1M |
| F2M |
| 2a | ||
|
| 2b | ||
|
| 2a | ||
|
| 2b | ||
|
| 4 |
| 5 |
| 4 |
| 5 |
| 1 |
| 4 |
利用a2+b2=c2,得c2=
| 5 |
| 4 |
| 1 |
| 4 |
因此,所求双曲线方程为x2-4y2=1.
(II)解:设点C(x1,y1),D(x2,y2),E(x3,y3),则直线l的方程为y=
| y1 |
| x1-m |
于是C(x1,y1)、D(x2,y2)两点坐标满足
|
将①代入②得(x12-2x1m+m2-4y12)x2+8my12x-4y12m2-x12+2mx1-m2=0.
由已知,显然m2-2x1m+1≠0.于是x1x2=-
| x12-2mx1+m2x12 |
| m2-2x1m+1 |
因为x1≠0,得x2=-
| x1-2m+m2x1 |
| m2-2x1m+1 |
同理,C(x1,y1)、E(x3,y3)两点坐标满足
|
可解得x3=-
x1-2
| ||||
(
|
| m2x1-2m+x1 |
| 1-2x1m+m2 |
所以x2=x3,故直线DE垂直于x轴.
点评:本小题主要考查双曲线的标准方程和几何性质、直线方程、平面向量、曲线和方程的关系等解析几何的基础知识和基本思想方法,考查推理及运算能力.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
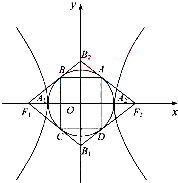 (2012•湖北)如图,双曲线
(2012•湖北)如图,双曲线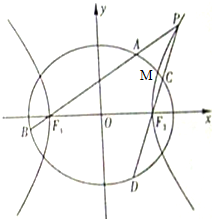 (2011•天津模拟)如图,椭圆
(2011•天津模拟)如图,椭圆 如图,双曲线C:
如图,双曲线C: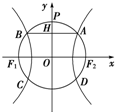 如图,双曲线
如图,双曲线