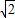题目内容

若x、y∈R，且x²+y²=1，则（1-xy）（1+xy）的最小值是，最大值是．

$\text{[math]}$ 1
分析：根据题意（1-xy）（1+xy）=1-x²y²，由不等式的基本性质可以求出x²y²的范围，从而求解．
解答：由题意（1-xy）（1+xy）=1-x²y²，
∴只要求出x²y²的范围即可，
∵x²+y²=1≥2 $\text{[math]}$ ，
∴x²y²≤ $\text{[math]}$ ，-x²y²≥- $\text{[math]}$ ，
∴（1-xy）（1+xy）=1-x²y²≥1- $\text{[math]}$ = $\text{[math]}$ ，
又∵x²y²＞0，
∴1-x²y²≤1，
∴（1-xy）（1+xy）的最小值是 $\text{[math]}$ ，最大值是 1，
故答案为 $\text{[math]}$ ，1．
点评：此题主要考查基本不等式的性质及其应用，是一道很好的题．