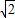题目内容
若x,y∈R,且x2+y2=1.当x+y+c=0时,c的最大值是( )
A.
| B.-
| C.2
| D.-2
|
根据题意设y=cosα,x=sinα,
将x+y+c=0变形为c=-x-y=-cosα-sinα=-
sin(α+
),
∴-
≤c≤
,
则c的最大值为
.
故选A
将x+y+c=0变形为c=-x-y=-cosα-sinα=-
| 2 |
| π |
| 4 |
∴-
| 2 |
| 2 |
则c的最大值为
| 2 |
故选A

练习册系列答案
相关题目