题目内容
17．已知（2-$\sqrt{3}$x）3=a0+a1x+a2x2+a3x3，则（a0+a2）2-（a1+a3）2=1．分析 构造函数，利用赋值法，通过平方差法，化简求解即可．
解答 解：令f（x）=（2-$\sqrt{3}$x）3=a0+a1x+a2x2+a3x3，
则f（1）=a0+a1+a2+a3=（2-$\sqrt{3}$）3．
f（-1）=a0-a1+a2-a3=（2+$\sqrt{3}$）3．
（a0+a2）2-（a1+a3）2=（a0+a1+a2+a3）（a0-a1+a2-a3）=（2-$\sqrt{3}$）3（2+$\sqrt{3}$）3=1．
故答案为：1．
点评 本题考查二项式定理的应用，考查赋值法以及平方差法的应用，考查计算能力．
练习册系列答案
相关题目
7．
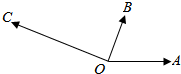如图，|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1，|$\overrightarrow{OC}$|=$\sqrt{3}$，∠AOB=60°，$\overrightarrow{OB}⊥\overrightarrow{OC}$，设$\overrightarrow{OC}=x\overrightarrow{OA}$+y$\overrightarrow{OB}$，则x，y的值分别为（ ）
如图，|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1，|$\overrightarrow{OC}$|=$\sqrt{3}$，∠AOB=60°，$\overrightarrow{OB}⊥\overrightarrow{OC}$，设$\overrightarrow{OC}=x\overrightarrow{OA}$+y$\overrightarrow{OB}$，则x，y的值分别为（ ）| A． | x=-2，y=-1 | B． | x=-2，y=1 | C． | x=2，y=-1 | D． | x=2，y=1 |
2．已知异面直线a，b成60°角，A为空间中一点，则过A与a，b都成45°角的平面（ ）
| A． | 有且只有一个 | B． | 有且只有两个 | C． | 有且只有三个 | D． | 有且只有四个 |
9．设a∈R，且（1+ai）2i为正实数，则a=（ ）
| A． | 0 | B． | -1 | C． | ±1 | D． | 1 |
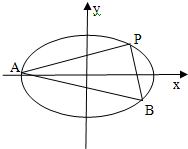已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）经过点P（2，1），且两焦点与短轴的一个端点构成等腰直角三角形．