题目内容
17.已知非空集合A={x|a<x<2a+3},B={x|0<x<1}(1)若a=-$\frac{1}{2}$,求 A∩B
(2)若A∩B=∅,求实数a的取值范围.
分析 (1)把a的值代入确定出A,求出A与B的交集即可;
(2)根据A与B的交集为空集,确定出a的范围即可.
解答 解:(1)把a=-$\frac{1}{2}$代入得:A={x|-$\frac{1}{2}$<x<2},
∵B={x|0<x<1},
∴A∩B={x|0<x<1};
(2)∵A∩B=∅,
∴A=∅或2a+3≤0或a≥1,
解得:a≤-3或a≤-$\frac{3}{2}$或a≥1,
则a的范围是a≤-$\frac{3}{2}$或a≥1.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
 如图,在三棱台ABO-A1B1O1中,侧面AOO1A1与侧面OBB1O1是全等的直角梯形,且OO1⊥OB,OO1⊥OA,平面AOO1A1⊥平面OBB1O1,OB=3,O1B1=1,OO1=$\sqrt{3}$.
如图,在三棱台ABO-A1B1O1中,侧面AOO1A1与侧面OBB1O1是全等的直角梯形,且OO1⊥OB,OO1⊥OA,平面AOO1A1⊥平面OBB1O1,OB=3,O1B1=1,OO1=$\sqrt{3}$.
 ,函数
,函数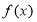 与
与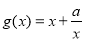 有相同极值点.
有相同极值点.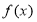 的最大值;
的最大值;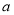 的值;
的值;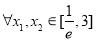 ,不等式
,不等式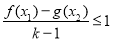 恒成立,求实数
恒成立,求实数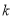 的取值范围.
的取值范围. 是
是 上的增函数,则实数
上的增函数,则实数 的取值范围是 .
的取值范围是 . .
. ,求函数
,求函数 在
在 处切线方程;
处切线方程; ,
, ,则
,则 等于( )
等于( ) B.
B.
 D.
D.