题目内容
4.在△ABC中,内角A,B,C的对边分别是a,b,c,若bsinB-asinA=$\frac{1}{2}$asinC,且△ABC的面积为a2sinB,则cosB=$\frac{3}{4}$.分析 由正弦定理化简已知的式子,结合条件和三角形的面积公式列出方程化简后,得到三边a、b、c的关系,由余弦定理求出cosB的值.
解答 解:∵bsinB-asinA=$\frac{1}{2}$asinC,
∴由正弦定理得,b2-a2=$\frac{1}{2}$ac,①
∵△ABC的面积为a2sinB,
∴$\frac{1}{2}acsinB={a}^{2}sinB$,则c=2a,
代入①得,b2=2a2,
由余弦定理得,cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$
=$\frac{{a}^{2}+4{a}^{2}-2{a}^{2}}{4{a}^{2}}$=$\frac{3}{4}$,
故答案为:$\frac{3}{4}$.
点评 本题考查正弦定理、余弦定理,以及三角形的面积公式的应用,考查转化思想,化简、变形能力.

练习册系列答案
相关题目
15.若命题:p∨q为真,且¬p为真,则( )
| A. | p∧q为真 | B. | p为真 | C. | q为假 | D. | q为真 |
12.某地区2007年至2013年农村居民家庭人均纯收入y(单位:千元)的数据如下表:
y关于t的线性回归方程为$\widehaty=0.5t+2.3$,则a的值为4.8.
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | a | 5.2 | 5.9 |
9.已知△ABC中,a=1,$b=\sqrt{3}$,A=30°,则B等于( )
| A. | 30° | B. | 30°或150° | C. | 60° | D. | 60°或120° |
13.某程序框图如图所示,若该程序运行后输出的值是$\frac{25}{13}$,则( )
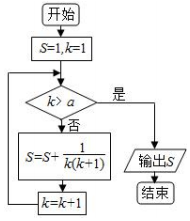

| A. | a=11 | B. | a=12 | C. | a=13 | D. | a=14 |
14.若不等式(a-1)x2-x+1>0对任意的x∈(0,+∞)恒成立,则实数a的取值范围是( )
| A. | [$\frac{5}{4}$,+∞) | B. | ($\frac{5}{4}$,+∞) | C. | [1,+∞) | D. | (1,+∞) |