题目内容
已知,a∈R,函数f(x)=x|x-a|.
(1)当a>2时,求函数y=f(x)在区间[1,2]上的最小值;
(2)设a≠0,若函数f(x)在(m,n)上既有最大值又有最小值,请分别求出m、n的取值范围.(用a表示)
(1)当a>2时,求函数y=f(x)在区间[1,2]上的最小值;
(2)设a≠0,若函数f(x)在(m,n)上既有最大值又有最小值,请分别求出m、n的取值范围.(用a表示)
分析:(1)化简函数f(x)的解析式为-(x-
)2+
,分
∈[1,2]、
>2 两种情况,分别求出它的最小值.
(2)a≠0,f(x)=
,分a>0和a<0两种情况,分别画出函数f(x)的图象,结合图象,根据题中要求,分别求出m、n的取值范围.
| a |
| 2 |
| a2 |
| 4 |
| a |
| 2 |
| a |
| 2 |
(2)a≠0,f(x)=
|
解答:解:(1)∵a>2,x∈[1,2],∴f(x)=x|x-a|=-x2+ax=-(x-
)2+
.
由于 4≥a>2,即当
∈[1,2]时,则当 x=
时,fmin(x)=
.
当
>2 时,即a>4时,f(x)在∈[1,2]上是减函数,
当x=2时,f(x)有最小值为fmin(x)=-(2-
)2+
=2a-4.
综上可得,fmin(x)=
.
(2)a≠0,f(x)=
.
①当a>0时,f(x)的图象如图1所示:显然函数f(x)在(-∞,a)上的最大值为f(
)=
.
由
,解得x=
a.
由于函数f(x)在(m,n)上既有最大值又有最小值,∴0≤m<
,a<n≤
a.
图1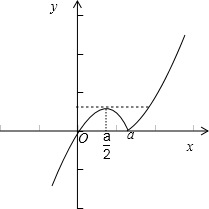 图2
图2 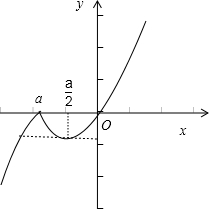
②当a<0时,如图2所示:显然函数f(x)在(a,+∞)上的最小值为f(
)=-
.
由
解得 x=
a.
由于函数f(x)在(m,n)上既有最大值又有最小值,故有
a≤m<a,
<n≤0.
| a |
| 2 |
| a2 |
| 4 |
由于 4≥a>2,即当
| a |
| 2 |
| a |
| 2 |
| a2 |
| 4 |
当
| a |
| 2 |
当x=2时,f(x)有最小值为fmin(x)=-(2-
| a |
| 2 |
| a2 |
| 4 |
综上可得,fmin(x)=
|
(2)a≠0,f(x)=
|
①当a>0时,f(x)的图象如图1所示:显然函数f(x)在(-∞,a)上的最大值为f(
| a |
| 2 |
| a2 |
| 4 |
由
|
1+
| ||
| 2 |
由于函数f(x)在(m,n)上既有最大值又有最小值,∴0≤m<
| a |
| 2 |
1+
| ||
| 2 |
图1
 图2
图2 
②当a<0时,如图2所示:显然函数f(x)在(a,+∞)上的最小值为f(
| a |
| 2 |
| a2 |
| 4 |
由
|
1-
| ||
| 2 |
由于函数f(x)在(m,n)上既有最大值又有最小值,故有
1-
| ||
| 2 |
| a |
| 2 |
点评:本题主要考查带有绝对值的函数图象和性质,二次函数的性质应用,体现了分类讨论和数形结合的数学思想,
属于中档题.
属于中档题.

练习册系列答案
相关题目