题目内容
3.已知函数f(x)=$\sqrt{3}$sinx+cosx在x0处取得最大值,则cos(x0-π)=-$\frac{1}{2}$.分析 f(x)解析式利用两角和与差的正弦函数公式化为一个角的正弦函数,由x=x0时,函数f(x)取得最大值,得到x0,然后求解cos(x0-π)的值.
解答 解:函数f(x)=$\sqrt{3}$sinx+cosx=2( $\frac{\sqrt{3}}{2}$sinx+$\frac{1}{2}$cosx)=2sin(x+$\frac{π}{6}$)
∵函数f(x)=$\sqrt{3}$sinx+cosx在x0处取得最大值,
∴sin(x0+$\frac{π}{6}$)=1,不妨x0=$\frac{π}{3}$+2kπ.
cos(x0-π)=-cosx0=-$\frac{1}{2}$.
故答案为:-$\frac{1}{2}$.
点评 此题考查了两角和与差的正弦函数公式,同角三角函数间的基本关系,以及正弦函数的定义域与值域,熟练掌握公式是解本题的关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
14.某企业为了更好地了解设备改造前后与生产合格品的关系,随机抽取了180件产品进行分析,其中设备改造前的合格品有36件,不合格品有49件,设备改造后生产的合格品有65件,不合格品有30件.根据所给数据:
(1)写出2×2列联表; (2)判断产品是否合格与设备改造是否有关,说明理由.
附:K2=$\frac{n(ad-bc)2}{(a+b)(c+d)(a+c)(b+d)}$,
数据支持:(65×49-36×30)2=4431025 101×79×85×95=64430825.
(1)写出2×2列联表; (2)判断产品是否合格与设备改造是否有关,说明理由.
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
数据支持:(65×49-36×30)2=4431025 101×79×85×95=64430825.
18.在区间[0,π]上随机地取一个x,则事件“$0≤sinx≤\frac{{\sqrt{2}}}{2}$”发生的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}}}{4}$ |
8.为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球时间x单位:小时)与当天投篮命中率y之间的关系:
(1)用线性回归分析的方法求回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$.(2)预测小李该月6号打6小时篮球的投篮命中率.
$\left\{\begin{array}{l}{\stackrel{∧}{b}=\frac{\sum_{i-1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i-1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}}\\{\stackrel{∧}{a}=\overline{y}-\stackrel{∧}{b}\overline{x}}\end{array}\right.$.
| 时间x | 1 | 2 | 3 | 4 | 5 |
| 命中率y | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
$\left\{\begin{array}{l}{\stackrel{∧}{b}=\frac{\sum_{i-1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i-1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}}\\{\stackrel{∧}{a}=\overline{y}-\stackrel{∧}{b}\overline{x}}\end{array}\right.$.
15.为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球时间x(单位:小时)与当天投篮命中率y之间的关系:
小李这5天的平均投篮命中率;用线性回归分析的方法,预测小李该月6号打6小时篮球的投篮命中率.
附:线性回归方程$\widehaty=\widehatbx+\widehata$中系数计算公式$\widehatb=\frac{{\sum_{i=1}^n{({x_i}-\overline x)}({y_i}-\overline y)}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
| 时间x | 1 | 2 | 3 | 4 | 5 |
| 命中率y | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
附:线性回归方程$\widehaty=\widehatbx+\widehata$中系数计算公式$\widehatb=\frac{{\sum_{i=1}^n{({x_i}-\overline x)}({y_i}-\overline y)}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
12.某城市2014年的空气质量状况如表所示:
其中污染指数T≤50时,空气质量为优;50<T≤100时,空气质量为良;100<T≤150时,空气质量为轻微污染,则该城市2014年空气质量达到良或优的概率为$\frac{3}{5}$.
| 污染指数T | 30 | 60 | 100 | 110 | 130 | 140 |
| 概率P | $\frac{1}{10}$ | $\frac{1}{6}$ | $\frac{1}{3}$ | $\frac{7}{30}$ | $\frac{2}{15}$ | $\frac{1}{30}$ |
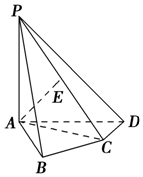 如图,在四棱锥PABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
如图,在四棱锥PABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.