题目内容
(本小题满分12分) 已知圆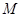 过两点
过两点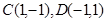 ,且圆心
,且圆心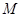 在
在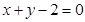 上.
上.
(1)求圆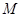 的方程;
的方程;
(2)设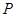 是直线
是直线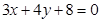 上的动点,
上的动点,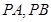 是圆
是圆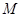 的两条切线,
的两条切线,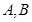 为切点,求四边形
为切点,求四边形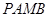 面积的最小值.
面积的最小值.
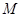 过两点
过两点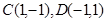 ,且圆心
,且圆心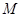 在
在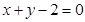 上.
上.(1)求圆
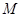 的方程;
的方程;(2)设
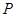 是直线
是直线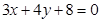 上的动点,
上的动点,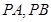 是圆
是圆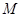 的两条切线,
的两条切线,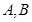 为切点,求四边形
为切点,求四边形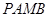 面积的最小值.
面积的最小值.(1) (x-1)2+(y-1)2=4. (2) S=2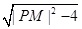 =2
=2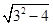 =2
=2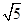 .
.
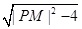 =2
=2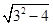 =2
=2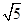 .
. 试题分析:(1)根据题意,设出圆心(a,b),然后圆
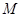 过两点
过两点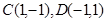 ,其中垂线必定过圆心,且圆心
,其中垂线必定过圆心,且圆心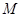 在
在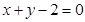 上.联立直线的方程组得到交点坐标即为圆心坐标,进而两点距离公式求解半径,得到圆的方程。
上.联立直线的方程组得到交点坐标即为圆心坐标,进而两点距离公式求解半径,得到圆的方程。(2)因为四边形PAMB的面积S=S△PAM+S△PBM=
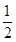 |AM|·|PA|+
|AM|·|PA|+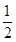 |BM|·|PB|,根据两个三三角形的底相同,高相等,那么即可知S=2|PA|,只需要求解切线长|PA|的最小值即可。
|BM|·|PB|,根据两个三三角形的底相同,高相等,那么即可知S=2|PA|,只需要求解切线长|PA|的最小值即可。解:(1)设圆
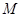 的方程为:(x-a)2+(y-b)2=r2(r>0).
的方程为:(x-a)2+(y-b)2=r2(r>0).根据题意,得
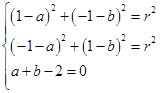 ﹍﹍﹍﹍﹍﹍﹍3分
﹍﹍﹍﹍﹍﹍﹍3分解得a=b=1,r=2, ﹍﹍﹍﹍﹍﹍﹍5分
故所求圆M的方程为(x-1)2+(y-1)2=4. ﹍﹍﹍﹍﹍﹍﹍6分
(2)因为四边形PAMB的面积S=S△PAM+S△PBM=
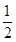 |AM|·|PA|+
|AM|·|PA|+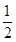 |BM|·|PB|,
|BM|·|PB|,又|AM|=|BM|=2,|PA|=|PB|, 所以S=2|PA|, ﹍﹍﹍﹍﹍﹍﹍8分而|PA|=
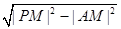 =
=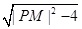 , 即S=2
, 即S=2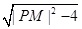 .
.因此要求S的最小值,只需求|PM|的最小值即可,
即在直线3x+4y+8=0上找一点P,使得|PM|的值最小,﹍﹍﹍﹍﹍﹍﹍9分
所以|PM|min=
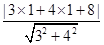 =3, ﹍﹍﹍﹍﹍﹍﹍10分
=3, ﹍﹍﹍﹍﹍﹍﹍10分所以四边形PAMB面积的最小值为S=2
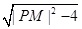 =2
=2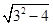 =2
=2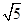 . ﹍﹍﹍12分
. ﹍﹍﹍12分点评:结合该试题的关键是理解圆心和半径是求解圆的方程核心,同时直线与圆相切时,构成的四边形的面积问题,能否转化为一条切线和一个半径以及一个圆心到圆外一点P的三角形的面积的最值,最终化简为只需要求解切线长|PA|的最小值即可。。

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 ,圆心在直线
,圆心在直线 上,且被直线
上,且被直线 截得的弦长为
截得的弦长为 ,求圆C的方程
,求圆C的方程 发出的一束光线,经
发出的一束光线,经 轴反射后,反射光线恰好平分圆:
轴反射后,反射光线恰好平分圆:
 的圆周,则反射光线所在的直线方程为 .
的圆周,则反射光线所在的直线方程为 .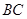 是圆
是圆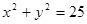 的动弦,且
的动弦,且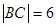 ,则
,则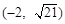 作圆C:
作圆C: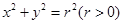 的切线,切点为D,且QD=4.
的切线,切点为D,且QD=4.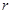 的值;
的值;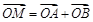 ,求
,求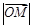 的最小值(O为坐标原点).
的最小值(O为坐标原点).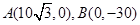 ,一圆心位于(0,3),半径为3的动圆沿x轴向右滚动,动圆每6秒滚动一圈,则动圆与直线AB第一次相切时所用的时间为 秒.
,一圆心位于(0,3),半径为3的动圆沿x轴向右滚动,动圆每6秒滚动一圈,则动圆与直线AB第一次相切时所用的时间为 秒.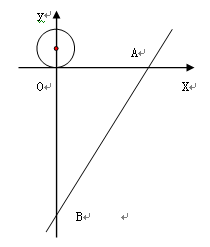
 作直线
作直线 与圆
与圆 相交于
相交于 两点,那么
两点,那么 的最小值为( )
的最小值为( )



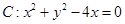 ,
,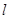 过点
过点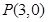 的直线,则
的直线,则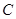 的位置关系是___________(填“相交”、“相切”、“相离”或“三种位置关系均有可能”).
的位置关系是___________(填“相交”、“相切”、“相离”或“三种位置关系均有可能”).