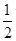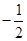题目内容
已知等差数列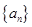 中,
中,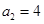 ;
;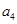 是
是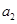 与
与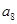 的等比中项.
的等比中项.
(I)求数列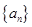 的通项公式:
的通项公式:
(II)若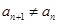 .求数列
.求数列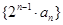 的前
的前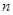 项和.
项和.
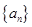 中,
中,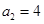 ;
;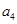 是
是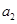 与
与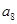 的等比中项.
的等比中项.(I)求数列
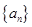 的通项公式:
的通项公式:(II)若
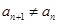 .求数列
.求数列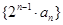 的前
的前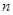 项和.
项和.(I)当 时,
时, ;当
;当 时,
时, ;(II)
;(II) .
.
 时,
时, ;当
;当 时,
时, ;(II)
;(II) .
.试题分析:(I)通过已知
 ,可以设公差为
,可以设公差为 ,然后根据等比中项的概念列出等式
,然后根据等比中项的概念列出等式 解出公差
解出公差 或
或 ,所以当
,所以当 时,
时, ;当
;当 时,
时, ;(II)根据条件可以确定
;(II)根据条件可以确定 的通项公式
的通项公式 ,则
,则 ,然后用错位相减法解出
,然后用错位相减法解出 .
.试题解析:(I)由题意,
 ,即
,即 ,化简得
,化简得  ,∴
,∴ 或
或
∵
 ,∴当
,∴当 时,
时, ;当
;当 时,
时, .
.(II)∵
 ,∴
,∴ ,∴
,∴ ,∴
,∴ ……①
……①①
 2,得
2,得 ……②,①-②,得
……②,①-②,得 =
= ,∴
,∴ .
.
练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
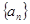 的公比为
的公比为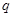 ,
,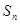 是
是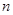 项和.
项和.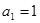 ,
,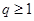 ,求
,求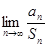 的值;
的值;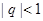 ,
,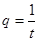 ,若首项
,若首项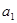 和
和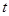 都是正整数,
都是正整数,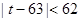 ,且对于任意正整数
,且对于任意正整数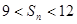 成立,问:这样的数列
成立,问:这样的数列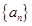 为等差数列,
为等差数列,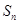 为其前
为其前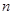 项和,且
项和,且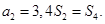
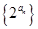 是等比数列;
是等比数列;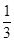 )是函数
)是函数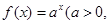 且
且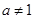 )的图象上一点,等比数列
)的图象上一点,等比数列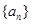 的前
的前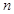 项和为
项和为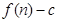 ,数列
,数列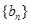
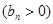 的首项为
的首项为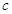 ,且前
,且前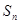 满足
满足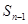 =
=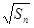 +
+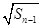 (
(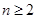 ).
).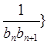 前
前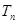 ,问
,问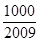 的最小正整数
的最小正整数 满足
满足
 .
.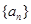 满足公比
满足公比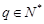 ,
,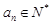 ,且{
,且{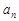 }中的任意两项之积也是该数列中的一项,若
}中的任意两项之积也是该数列中的一项,若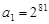 ,则
,则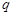 的所有可能取值的集合为 .
的所有可能取值的集合为 .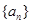 的公比
的公比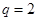 ,则
,则 .
.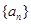 中,
中,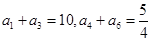 ,则公比
,则公比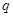 等于( )
等于( )