Question

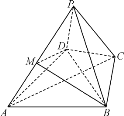
【题目】如图，在四棱锥PABCD中，M是PA上的点，为正三角形，，．

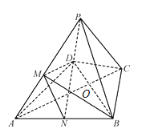
（1）求证：平面平面PAC；

（2）若，平面BPC，求证：点M为线段PA的中点．

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】

（1）取BD的中点O，连结OA，OC，可证，又由，可得平面PAC，即可得证；

（2）取AB的中点N，连结MN和DN，首先可得，，所以，即可得到平面BPC．又由平面BPC，可得平面平面BPC．根据面面平行的性质可得，即可得证；

（1）取BD的中点O，连结OA，OC，

∵为正三角形，∴．

∵，∴．

在平面内，过O点垂直于BD的直线有且只有一条，

∴A，O，C三点共线，即．

∵，AC，平面PAC，，

∴平面PAC．∵平面MBD，

∴平面平面PAC．

（2）取AB的中点N，连结MN和DN，

因为，且，所以

所以，即．

∵为正三角形，∴．

又DN，BC，AB共面，∴．

∵平面BPC，平面BPC，

∴平面BPC．

∵平面BPC，DN，平面DMN，

∴平面平面BPC．

∵平面DMN，∴平面BPC．

∵平面PAB，平面平面BPC=PB，

∴．

∵N是AB的中点，∴M为线段PA的中点．