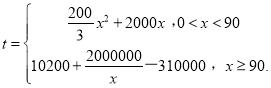题目内容
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() 为参数),在以坐标原点
为参数),在以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,点
轴的正半轴为极轴的极坐标系中,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
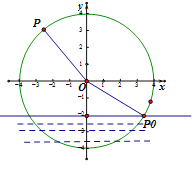
(2)若![]() 是曲线
是曲线![]() 上的动点,
上的动点,![]() 为线段
为线段![]() 的中点,求点
的中点,求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用极坐标与直角坐标互化公式即可求得直线![]() 的直角坐标方程,将曲线C的参数方程消参数
的直角坐标方程,将曲线C的参数方程消参数![]() 即可求得曲线
即可求得曲线![]() 的普通方程,问题得解。
的普通方程,问题得解。
(2)求出点![]() 的直角坐标,再利用椭圆的参数方程表示点
的直角坐标,再利用椭圆的参数方程表示点![]() 的坐标为
的坐标为![]() ,利用点到直线距离公式及两角差的正弦公式即可整理点P到直线
,利用点到直线距离公式及两角差的正弦公式即可整理点P到直线![]() 的距离
的距离![]() ,问题得解。
,问题得解。
(1)因为直线![]() 的极坐标方程为
的极坐标方程为![]() ,
,
即ρsinθ-ρcosθ+4=0.
由x=ρcosθ,y=ρsinθ,
可得直线![]() 的直角坐标方程为x-y-4=0.
的直角坐标方程为x-y-4=0.
将曲线C的参数方程![]() 消去参数
消去参数![]() ,
,
得曲线C的普通方程为![]() .
.
(2)设N(![]() ,sinα),α∈[0,2π).
,sinα),α∈[0,2π).
点M的极坐标(![]() ,
,![]() )化为直角坐标为(-2,2).
)化为直角坐标为(-2,2).
则![]() .
.
所以点P到直线![]() 的距离
的距离![]() ,
,
所以当![]() 时,点M到直线
时,点M到直线![]() 的距离的最大值为
的距离的最大值为![]() .
.

练习册系列答案
相关题目
【题目】下表是某地某年月平均气温(华氏度):
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
平均气温 | 21.4 | 26.0 | 36.0 | 48.8 | 59.1 | 68.6 | 73.0 | 71.9 | 64.7 | 53.5 | 39.8 | 27.7 |
以月份为x轴(![]() 月份
月份![]() ),以平均气温为y轴.
),以平均气温为y轴.
(1)用正弦曲线去拟合这些数据;
(2)估计这个正弦曲线的周期T和振幅A;
(3)下面三个函数模型中,哪一个最适合这些数据?
①![]() ;②
;②![]() ;③
;③![]() .
.