题目内容
【题目】已知函数 ![]() ,
, ![]() ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(1)求函数 ![]() 在x
在x ![]() 1处的切线方程;
1处的切线方程;
(2)若存在 ![]()
![]() ,使得
,使得 ![]() 成立,其中
成立,其中 ![]() 为常数,
为常数,
求证: ![]() ;
;
(3)若对任意的 ![]() ,不等式
,不等式 ![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【答案】
(1)
解:(1)因为 ![]() ,所以
,所以 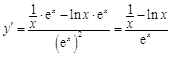 ,故
,故 ![]() .
.
所以函数 ![]() 在x
在x ![]() 1处的切线方程为
1处的切线方程为 ![]() ,
,
即 ![]() .
.
(2)
由已知等式 ![]() 得
得 ![]() .
.
记 ![]() ,则
,则 ![]() .
.
假设 ![]() .
.
①若 ![]() ,则
,则 ![]() ,所以
,所以 ![]() 在
在 ![]() 上为单调增函数.
上为单调增函数.
又 ![]() ,所以
,所以 ![]() ,与
,与 ![]() 矛盾.
矛盾.
②若 ![]() ,记
,记 ![]() ,则
,则 ![]() .
.
令 ![]() ,解得
,解得 ![]() .
.
当 ![]() 时,
时, ![]() ,
, ![]() 在
在 ![]() 上为单调增函数;
上为单调增函数;
当 ![]() 时,
时, ![]() ,
, ![]() 在
在 ![]() 上为单调减函数.
上为单调减函数.
所以 ![]() ,所以
,所以 ![]() ,
,
所以 ![]() 在
在 ![]() 上为单调增函数.
上为单调增函数.
又 ![]() ,所以
,所以 ![]() ,与
,与 ![]() 矛盾.
矛盾.
综合①②,假设不成立,所以 ![]() .
.
(3)
由 ![]() 得
得 ![]() .
.
记 ![]() ,
, ![]() ,
,
则 ![]() .
.
①当 ![]() 时,因为
时,因为 ![]() ,
, ![]() ,所以
,所以 ![]() ,
,
所以 ![]() 在
在 ![]() 上为单调增函数,所以
上为单调增函数,所以 ![]() ,
,
故原不等式恒成立.
法一:
②当 ![]() 时,由(2)知
时,由(2)知 ![]() ,
, ![]() ,
,
当 ![]() 时,
时, ![]() ,
, ![]() 为单调减函数,
为单调减函数,
所以 ![]() ,不合题意.
,不合题意.
法二:
②当 ![]() 时,一方面
时,一方面 ![]() .
.
另一方面, ![]() ,
, ![]() .
.
所以 ![]() ,使
,使 ![]() ,又
,又 ![]() 在
在 ![]() 上为单调减函数,
上为单调减函数,
所以当 ![]() 时,
时, ![]() ,故
,故 ![]() 在
在 ![]() 上为单调减函数,
上为单调减函数,
所以 ![]() ,不合题意.
,不合题意.
综上, ![]() .
.
【解析】(1.)利用积函数的导函数法则求出导函数再将x=1代入求出斜率求出切线方程。
(2.)假设 ![]() ,将
,将 ![]() 整理为
整理为 ![]() ,求导又单调性判断是否在不同点存在相同的y值
,求导又单调性判断是否在不同点存在相同的y值
(3.)对 ![]() 求导然后分
求导然后分 ![]() 、
、 ![]() 两种情况讨论。
两种情况讨论。
【考点精析】本题主要考查了复合函数单调性的判断方法的相关知识点,需要掌握复合函数f[g(x)]的单调性与构成它的函数u=g(x),y=f(u)的单调性密切相关,其规律:“同增异减”才能正确解答此题.

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案【题目】现有1 000根某品种的棉花纤维,从中随机抽取50根,纤维长度(单位:mm)的数据分组及各组的频数见右上表,据此估计这1 000根中纤维长度不小于37.5 mm的根数是 .
纤维长度 | 频数 |
[22.5,25.5) | 3 |
[25.5,28.5) | 8 |
[28.5,31.5) | 9 |
[31.5,34.5) | 11 |
[34.5,37.5) | 10 |
[37.5,40.5) | 5 |
[40.5,43.5] | 4 |