Question

【题目】平面直角坐标系xOy中，椭圆C： =1（a＞b＞0）的长轴长为2，抛物线E：x2=2y的准线与椭圆C相切．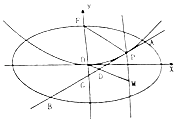

（Ⅰ）求椭圆C的方程；
（Ⅱ）若直线l与椭圆C相交于A，B两点且与抛物线E在第一象限相切于点P，线段AB的中点为D，直线OD与过P且垂直于x轴的直线交于点M，求 的最小值及此时点P的坐标．

Answer 1

【答案】解：（Ⅰ）由题意可知2a=2，b= ，∴椭圆C的方程为：x2+4y2=1．
（Ⅱ）设P（x0 ， y0），（x0＞0）可得 ，由y= x2的导数为y′=x，即有切线的斜率为x0 ，
则切线的方程为y﹣y0=x0（x﹣x0），
直线l的方程为y=x0x﹣y0 ， 令x=0，可得G（0，﹣y0），
则S△PFG= |FG||x0|= x0（ +y0）= x0（1+x02）；
∵|OG|=y0 ，∴ = ≥1，
当且仅当x0=1时，即P（1， ）时， 有最小值1
【解析】（Ⅰ）运用椭圆的长轴和抛物线的准线，以及椭圆的a，b，c的关系，解得a，b，进而得到椭圆的方程；（Ⅱ）设P（x0 ， y0），运用导数求得切线的斜率和方程，令x=0，可得点G的坐标，S△PFG= |FG||x0|= x0（ +y0）= x0（1+x02）； = 即可．
【考点精析】利用椭圆的标准方程对题目进行判断即可得到答案，需要熟知椭圆标准方程焦点在x轴：，焦点在y轴：．