题目内容
16.设已知函数f(x)=|log2x|,正实数m,n满足m<n,且f(m)=f(n),若f(x)在区间[m,n2]上的最大值为4,则n+m=$\frac{17}{4}$.分析 由题意可知-log2m=log2n,从而可得mn=1;从而解得.
解答 解:∵y=log2x在其定义域上单调递增,
又∵f(x)=|log2x|,且m<n,f(m)=f(n),
∴-log2m=log2n,
∴mn=1;
∵f(x)在区间[m,n2]上的最大值为4,
∴2log2n=4,
故n=4,m=$\frac{1}{4}$,n+m=$\frac{17}{4}$;
故答案为:$\frac{17}{4}$.
点评 本题考查了对数函数的性质应用及绝对值函数的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.圆O中,弦AB满足|AB|=2,则$\overrightarrow{AB}$•$\overrightarrow{AO}$=( )
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | 4 |
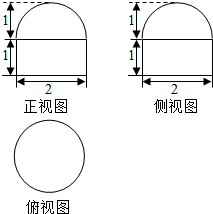 已知一个空间组合体的三视图如图所示,其中正视图、侧视图都是由半圆和矩形组成,请说出该组合体由哪些几何体组成,并且求出该组合体的表面积和体积.
已知一个空间组合体的三视图如图所示,其中正视图、侧视图都是由半圆和矩形组成,请说出该组合体由哪些几何体组成,并且求出该组合体的表面积和体积.