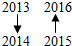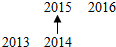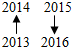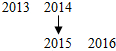题目内容
7.已知集合A={x|x2-x-6<0},集合B={x|x2+2x-8>0},集合C={x|x2-4ax+3a2<0},若C?(A∩B),试确定实数a的取值范围[1,2].分析 先确定集合A,B得到A={x|-2<x<3},B={x|x<-4或x>2},再根据题意分类讨论得出a的取值范围.
解答 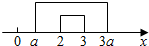 解:由已知得A={x|-2<x<3},B={x|x<-4或x>2},
解:由已知得A={x|-2<x<3},B={x|x<-4或x>2},
所以,A∩B={x|2<x<3},
C={x|x2-4ax+3a2<0}={x|(x-a)(x-3a)<0},
①当a>0时,C={x|a<x<3a},如右图所示:
则C?(A∩B)等价为:$\left\{\begin{array}{l}{a≤2}\\{3a≥3}\end{array}\right.$,
解得,1≤a≤2,经检验符合题意;
②当a<0时,C={x|3a<x<a};
C是负半轴上的一个区间,而A∩B是正半轴上的一个区间,
因此C?(A∩B)是不可能的,故无解;
③当a=0时,C=∅,此时C?(A∩B)是不可能的,也无解.
综合以上讨论得,a∈[1,2].
故答案为:[1,2].
点评 本题主要考查了子集与交集的运算,涉及一元二次不等式的解法,体现了分类讨论的解题思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列命题中,正确的命题是( )
| A. | 若a>b,c>d,则ac>bd | B. | 若$\frac{1}{a}>\frac{1}{b}$,则 a<b | ||
| C. | 若b>c,则|a|b≥|a|c | D. | 若a>b,c>d,则a-c>b-d |
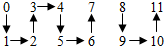 …,则从2013到2016四数之间的位置图形为( )
…,则从2013到2016四数之间的位置图形为( )