题目内容
函数y=
的值域是（ ）
| x2+1 |
| A、[0，+∞） |
| B、[1，+∞） |
| C、（0，+∞） |
| D、（1，+∞） |
考点：函数的值域
专题：函数的性质及应用
分析：通过函数的解析式，直接得到函数的值域即可．
解答：
解：函数y=
可知：
≥1，即y≥1．
所以函数的值域为：[1，+∞）．
故选：B．
| x2+1 |
| x2+1 |
所以函数的值域为：[1，+∞）．
故选：B．
点评：本题考查函数的值域的求法，基本知识的考查．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
已知函数y=f（x）是定义域为R的偶函数．当x≥0时，f（x）=
，若关于x的方程5[f（x）]2-（5a+6）f（x）+6a=0（a∈R），有且仅有6个不同实数根，则实数a的取值范围是（ ）
|
A、0＜a＜1或a=
| ||
B、0≤a≤1或a=
| ||
C、0＜a≤1或a=
| ||
D、1＜a≤
|
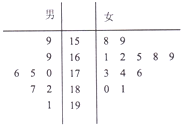第117届中国进出口商品交易会（简称2015年春季交广会）将于2015年4月15日在广州市举行，为了搞好接待工作，组委会在广州某大学分别招募8名男志愿者和12名女志愿者，现将这20名志愿者的身高组成如茎叶图（单位：m），若身高在175cm以上（包括175cm）定义为“高个子”，身高在175cm以下（不包括175cm）定义为“非高个子”．若椭圆的中心及两个焦点将两条准线之间的距离四等分，则椭圆的离心率为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|