题目内容
已知函数f(x)=
+lnx.
(Ⅰ)若函数f(x)在[1,+∞)上是增函数,求正实数a的取值范围;
(Ⅱ)若a=1,k∈R且k<
,设F(x)=f(x)+(k-1)lnx,求函数F(x)在[
,e]上的最大值和最小值.
| 1-x |
| ax |
(Ⅰ)若函数f(x)在[1,+∞)上是增函数,求正实数a的取值范围;
(Ⅱ)若a=1,k∈R且k<
| 1 |
| e |
| 1 |
| e |
(Ⅰ)由题设可得f′(x)=
(a>0)
因为函数f(x)在[1,+∞)上是增函数,所以当x∈[1,+∞)时,不等式f′(x)=
≥0,即a≥
恒成立
因为当x∈[1,+∞)时,
的最大值为1,所以实数a的取值范围是[1,+∞)-----(4分)
(Ⅱ)a=1时,f(x)=
+lnx,F(x)=
+lnx+(k-1)lnx=
+klnx
所以,F′(x)=
+
=
…(6分)
(1)若k=0,则F′(x)=
,在[
,e]上,恒有F'(x)<0,所以F(x)在[
,e]上单调递减
∴F(x)min=F(e)=
,F(x)max=F(
)=e-1…(7分)
(2)k≠0时,F′(x)=
=
(i)若k<0,在[
,e]上,恒有
<0,所以F(x)在[
,e]上单调递减
∴F(x)min=F(e)=
+klne=
+k=
+k-1,F(x)max=F(
)=e-k-1…(9分)
(ii)k>0时,因为k<
,所以
>e(x-
)<0,所以
<0,所以F(x)在[
,e]上单调递减
∴F(x)min=F(e)=
+klne=
+k=
+k-1,F(x)max=F(
)=e-k-1…(11分)
综上所述:当k=0时,F(x)min=
,F(x)max=e-1;当k≠0且k<
时,F(x)max=e-k-1,F(x)min=
+k-1.…(12分)
| ax-1 |
| ax2 |
因为函数f(x)在[1,+∞)上是增函数,所以当x∈[1,+∞)时,不等式f′(x)=
| ax-1 |
| ax2 |
| 1 |
| x |
因为当x∈[1,+∞)时,
| 1 |
| x |
(Ⅱ)a=1时,f(x)=
| 1-x |
| x |
| 1-x |
| x |
| 1-x |
| x |
所以,F′(x)=
| (1-x)′x-(1-x)x′ |
| x2 |
| k |
| x |
| kx-1 |
| x2 |
(1)若k=0,则F′(x)=
| -1 |
| x2 |
| 1 |
| e |
| 1 |
| e |
∴F(x)min=F(e)=
| 1-e |
| e |
| 1 |
| e |
(2)k≠0时,F′(x)=
| kx-1 |
| x2 |
k(x-
| ||
| x2 |
(i)若k<0,在[
| 1 |
| e |
k(x-
| ||
| x2 |
| 1 |
| e |
∴F(x)min=F(e)=
| 1-e |
| e |
| 1-e |
| e |
| 1 |
| e |
| 1 |
| e |
(ii)k>0时,因为k<
| 1 |
| e |
| 1 |
| k |
| 1 |
| k |
k(x-
| ||
| x2 |
| 1 |
| e |
∴F(x)min=F(e)=
| 1-e |
| e |
| 1-e |
| e |
| 1 |
| e |
| 1 |
| e |
综上所述:当k=0时,F(x)min=
| 1-e |
| e |
| 1 |
| e |
| 1 |
| e |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在R上可导,
在R上可导, ,则
,则 ( )
( )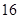


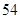
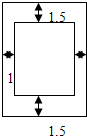
 与
与 轴,直线
轴,直线 围成的封闭图形的面积为( )
围成的封闭图形的面积为( )



 ,
, ,
, ,则
,则 的大小关系是( ).
的大小关系是( ).

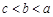

 在第一象限内围成的封闭图形的面积为( )
在第一象限内围成的封闭图形的面积为( )

