题目内容
1.若函数f(x)=ex+x-2,g(x)=lnx+x2-3,若f(a)=0,g(b)=0,则( )| A. | g(a)>f(b) | B. | g(a)<f(b) | C. | g(a)≤f(b) | D. | g(a)≥f(b) |
分析 先判断函数f(x)和g(x)在R上的单调性,再利用f(a)=0,g(b)=0判断a,b的取值范围即可.
解答 解:由于y=ex及y=x-2关于x是单调递增函数,∴函数f(x)=ex+x-2在R上单调递增.
分别作出y=ex,y=2-x的图象,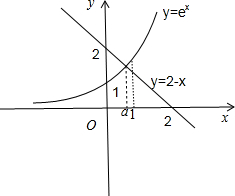
∵f(0)=1+0-2<0,f(1)=e-1>0,f(a)=0,
∴0<a<1.
同理g(x)=lnx+x2-3在R+上单调递增,
g(1)=ln1+1-3=-2<0,
由于g($\sqrt{3}$)=ln$\sqrt{3}$+($\sqrt{3}$)2-3=$\frac{1}{2}$ln3>0,
故由 g(b)=0,
可得1<b<$\sqrt{3}$.
∴g(a)=lna+a2-3<g(1)=ln1+1-3=-2<0,
f(b)=eb+b-2>f(1)=e+1-2=e-1>0.
∴g(a)<0<f(b).
故选:B.
点评 本题主要考查函数的单调性、不等式与不等关系,熟练掌握函数的单调性、函数零点的判定定理是解题的关键,体现了数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
16.已知全集为R,M={x|x(x-3)<0},N={x|x<1或x≥3},则正确的为( )
| A. | M⊆N | B. | N⊆M | C. | ∁RN⊆M | D. | M⊆∁RN |
6.已知?ABCD的三个顶点的坐标分别是A(0,1),B(1,0),C(4,3),则顶点D的坐标为( )
| A. | (3,4) | B. | (4,3) | C. | (3,1) | D. | (3,8) |
13.已知P是椭圆$\frac{{x}^{2}}{4}$+y2=1上的动点,则P点到直线l:x+y-2$\sqrt{5}$=0的距离的最小值为( )
| A. | $\frac{\sqrt{10}}{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{\sqrt{2}}{5}$ |
10.已知命题p:?x0∈R,x0-2>1gx0;命题q:?x∈R,x2+x+1>0,给出下列结论( )
①命题“p∧q”是真命题;
②命题“p∧(¬q)”是假命题;
③命题“(¬p)∨q”是真命题;
④命题“p∨(¬q)”是假命题.
①命题“p∧q”是真命题;
②命题“p∧(¬q)”是假命题;
③命题“(¬p)∨q”是真命题;
④命题“p∨(¬q)”是假命题.
| A. | ②③ | B. | ①④ | C. | ①③④ | D. | ①②③ |
11.若cos θ=-$\frac{3}{5}$,且180°<θ<270°,则tan $\frac{θ}{2}$的值为( )
| A. | 2 | B. | -2 | C. | ±2 | D. | ±$\frac{1}{2}$ |