题目内容
11.从点(4,4)射出的光线,沿着向量$\overrightarrow{e}$=(-$\frac{2}{\sqrt{5}}$,-$\frac{1}{\sqrt{5}}$)的方向射到y轴上,经y轴反射后,反射光线必经过点( )| A. | (1,2) | B. | (2,2) | C. | (3,1) | D. | (4,0) |
分析 由题意求出向量$\overrightarrow{e}$=(-$\frac{2}{\sqrt{5}}$,-$\frac{1}{\sqrt{5}}$)的方向射到y轴上直线斜率k,可得点(4,4)射出的光线沿着向量$\overrightarrow{e}$=(-$\frac{2}{\sqrt{5}}$,-$\frac{1}{\sqrt{5}}$)的方向射到y轴上的直线方程,利用对称性求解反射光线的直线方程,考查各选项可得结论.
解答 解:由题意:向量$\overrightarrow{e}$=(-$\frac{2}{\sqrt{5}}$,-$\frac{1}{\sqrt{5}}$)的方向射到y轴上直线斜率k=$\frac{-\frac{1}{\sqrt{5}}}{-\frac{2}{\sqrt{5}}}=\frac{1}{2}$,
∴点(4,4)射出的光线沿着向量$\overrightarrow{e}$=(-$\frac{2}{\sqrt{5}}$,-$\frac{1}{\sqrt{5}}$)的方向射到y轴上的直线方程为y-4=$\frac{1}{2}$(x-4).
∵经过y轴的反射光线与y-4=$\frac{1}{2}$(x-4)关于y轴对称,
设反射光线的直线方程M(x,y)则关于y轴对称的N为(-x,y)
点N在直线y-4=$\frac{1}{2}$(x-4)上,
∴反射光线的直线方程为y-4=$\frac{1}{2}$(-x-4)
考查各选项可知:D点在反射光线上.
故选D.
点评 本题考查了直线方程的求法和直线关于直线对称的问题.属于中档题.

练习册系列答案
相关题目
19.若数列{an}满足a1=1,a2=2,an=an-1+an-2(n∈N*,n>2),则a6=( )
| A. | 13 | B. | 8 | C. | 21 | D. | 10 |
3.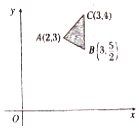 如图,已知点(x,y)在△ABC所包围的阴影部分区域内(包含边界),若B(3,$\frac{5}{2}$)是使得z=ax-y取得最大值的最优解,则实数a的取值范围为( )
如图,已知点(x,y)在△ABC所包围的阴影部分区域内(包含边界),若B(3,$\frac{5}{2}$)是使得z=ax-y取得最大值的最优解,则实数a的取值范围为( )
 如图,已知点(x,y)在△ABC所包围的阴影部分区域内(包含边界),若B(3,$\frac{5}{2}$)是使得z=ax-y取得最大值的最优解,则实数a的取值范围为( )
如图,已知点(x,y)在△ABC所包围的阴影部分区域内(包含边界),若B(3,$\frac{5}{2}$)是使得z=ax-y取得最大值的最优解,则实数a的取值范围为( )| A. | [-$\frac{1}{2}$,+∞) | B. | [0,+∞) | C. | (-∞,-$\frac{1}{2}$] | D. | [-$\frac{1}{2}$,0] |