题目内容
【题目】椭圆![]() 的左、右焦点分别是
的左、右焦点分别是![]() ,
,![]() ,离心率为
,离心率为![]() ,过
,过![]() 且垂直于
且垂直于![]() 轴的直线被椭圆
轴的直线被椭圆![]() 截得的线段长为1.
截得的线段长为1.
(1)求椭圆![]() 的方程;
的方程;
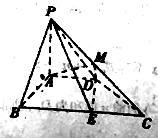
(2)点![]() 是椭圆
是椭圆![]() 上除长轴端点外的任一点,连接
上除长轴端点外的任一点,连接![]() ,
,![]() ,设
,设![]() 的角平分线
的角平分线![]() 交
交![]() 的长轴于点
的长轴于点![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() ,使得
,使得![]() 与椭圆
与椭圆![]() 有且只有一个公共点,设直线
有且只有一个公共点,设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,若
,若![]() ,证明
,证明![]() 为定值,并求出这个定值.
为定值,并求出这个定值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析,定值为
;(3)见解析,定值为![]() .
.
【解析】
(1)将![]() 代入椭圆
代入椭圆![]() 方程可得
方程可得![]() ,从而可得
,从而可得![]() ,再结合
,再结合![]() 及
及![]() ,即可求椭圆
,即可求椭圆![]() 的方程;
的方程;
(2)设![]() ,分别求出直线
,分别求出直线![]() ,
,![]() 的方程,利用角平分线的性质:角平分线上任一点到角两边的距离相等,列出关于
的方程,利用角平分线的性质:角平分线上任一点到角两边的距离相等,列出关于![]() 方程,结合
方程,结合![]() 消去
消去![]() ,将
,将![]() 用
用![]() 表示,利用
表示,利用![]() 的有界性即可求出
的有界性即可求出![]() 的范围;
的范围;
(3)将直线![]() 方程
方程![]() 与椭圆
与椭圆![]() 的方程联立,消去
的方程联立,消去![]() ,得到关于
,得到关于![]() 的一元二次方程,因
的一元二次方程,因![]() 与椭圆
与椭圆![]() 有且只有一个公共点,故由
有且只有一个公共点,故由![]() ,可求出
,可求出![]() ,再利用斜率公式求出
,再利用斜率公式求出![]() ,即可求出定值.
,即可求出定值.
(1)由于![]() ,将
,将![]() 代入椭圆方程
代入椭圆方程![]() ,得
,得![]() .
.
由题意知![]() ,即
,即![]() .
.
又![]() ,
,![]() ,所以
,所以![]() ,
,![]() .
.
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)设![]() ,又
,又![]() ,
,![]() ,所以直线
,所以直线![]() ,
,![]() 的方程分别为
的方程分别为
![]() ,
,![]() .
.
由题意知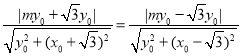 .
.
由于点![]() 在椭圆上,所以
在椭圆上,所以![]() .
.
所以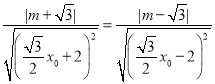 .
.
因为![]() ,
,![]() ,可得
,可得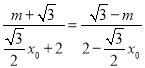 ,
,
所以![]() ,因此
,因此![]() .
.
(3)设![]() ,则直线
,则直线![]() 的方程为
的方程为![]() .
.
联立得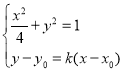 ,
,
整理得![]() .
.
由题意![]() ,即
,即![]() .
.
又![]() ,所以
,所以![]() ,故
,故![]() .
.
由(2)知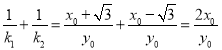 ,
,
所以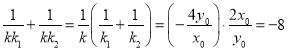 ,
,
因此![]() 为定值,这个定值为
为定值,这个定值为![]() .
.

练习册系列答案
相关题目