题目内容
【题目】已知数列![]() 是各项均为正数的等差数列,其中
是各项均为正数的等差数列,其中![]() ,且
,且![]() 成等比数列;数列
成等比数列;数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)如果![]() ,设数列
,设数列![]() 的前
的前![]() 项和为
项和为![]() ,是否存在正整数
,是否存在正整数![]() ,使得
,使得![]() 成立,若存在,求出
成立,若存在,求出![]() 的最小值,若不存在,说明理由.
的最小值,若不存在,说明理由.
【答案】(1)![]() ,
, ![]() ;(2)存在;
;(2)存在; ![]() 。
。
【解析】试题(1)数列![]() 是等差数列,
是等差数列, ![]() 用公差
用公差![]() 表示出来后,由已知求得
表示出来后,由已知求得![]() ,可得通项公式,数列
,可得通项公式,数列![]() 是已知和
是已知和![]() 与项
与项![]() 的关系,可由
的关系,可由![]() 求得
求得![]() ,再写出当
,再写出当![]() 时
时![]() ,两式相减后可得
,两式相减后可得![]() 的递推式
的递推式![]() ,从而知
,从而知![]() 是等比数列,由此可得通项公式;(2)数列
是等比数列,由此可得通项公式;(2)数列![]() 是由等差数列与等比数列相乘所得,其前
是由等差数列与等比数列相乘所得,其前![]() 项和
项和![]() 用错位相减法求得,由(2)得出
用错位相减法求得,由(2)得出![]() ,作差
,作差![]()
![]() ,会发现当
,会发现当![]() 时都有
时都有![]()
![]() ,因此结论是肯定的.
,因此结论是肯定的.
试题解析:(1)设数列![]() 的公差为
的公差为![]() ,依条件有
,依条件有![]() ,即
,即![]() ,
,
解得![]() (舍)或
(舍)或![]() ,
, ![]() ,由
,由![]() 得
得![]() ,
,
当![]() 时,
时, ![]() ,解得
,解得![]() ,当
,当![]() 时,
时, ![]() ,
,
![]() ,
, ![]() 数列
数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,故
的等比数列,故![]() ;
;
(2)由(1)知: ![]() ,
, ![]() ①,
①,
![]() ②,
②,
① —②得![]()
又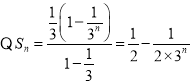 ,
, ![]() ,当
,当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() ,故所求的正整数
,故所求的正整数![]() 存在,其最小值为2.
存在,其最小值为2.

练习册系列答案
相关题目





