题目内容
已知函数f(x)=ax2+2x-2-a(a≤0),
(1)若a=-1,求函数的零点;
(2)若函数在区间(0,1]上恰有一个零点,求a的取值范围.
(1)若a=-1,求函数的零点;
(2)若函数在区间(0,1]上恰有一个零点,求a的取值范围.
考点:一元二次不等式的解法,二次函数的性质,函数零点的判定定理
专题:不等式的解法及应用
分析:(1)利用零点的含义、一元二次方程的解法即可得出;
(2))分类讨论:当a=0时,直接求出.当a<0,二次函数有且只有一个零点且在(0,1]时,满足条件,
,解出即可.
③当a<0,二次函数有两个零点,一个在(0,1]时,满足条件,
,
(2))分类讨论:当a=0时,直接求出.当a<0,二次函数有且只有一个零点且在(0,1]时,满足条件,
|
③当a<0,二次函数有两个零点,一个在(0,1]时,满足条件,
|
解答:
解:(1)当a=-1时,f(x)=-x2+2x-1,
令f(x)=-x2+2x-1=0,
解得x=1,
∴当a=-1时,函数f(x)的零点是1.
(2)①当a=0时,2x-2=0得x=1,符合题意.
当a≠0时,f(x)=a(x+
)2-2-a-
.△=4(a+1)2≥0.
②当-1<a<0,-
>1.二次函数有且只有一个零点且在(0,1]时,
则f(0)<0,f(1)=0,∴-2-a<0,解得-1<a<0.
③当a=-1时,f(x)=-(x-1)2=0,解得x=1,满足条件.
④当a<-1,则0<-
<1.f(0)=-2-a≤0,f(1)=0,解得-1>a≥-2.
综上可得:a∈[-2,0].
令f(x)=-x2+2x-1=0,
解得x=1,
∴当a=-1时,函数f(x)的零点是1.
(2)①当a=0时,2x-2=0得x=1,符合题意.
当a≠0时,f(x)=a(x+
| 1 |
| a |
| 1 |
| a |
②当-1<a<0,-
| 1 |
| a |
则f(0)<0,f(1)=0,∴-2-a<0,解得-1<a<0.
③当a=-1时,f(x)=-(x-1)2=0,解得x=1,满足条件.
④当a<-1,则0<-
| 1 |
| a |
综上可得:a∈[-2,0].
点评:本题主要考查了二次函数的性质,以及函数零点存在性定理,同时考查了运算求解的能力和分类讨论的思想方法,属于基础题.

练习册系列答案
相关题目
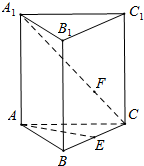 如图,已知正三棱柱ABC-A1B1C1的各棱长都是4,E是BC的中点,动点F在线段CA1上,且不与点C、A1重合.
如图,已知正三棱柱ABC-A1B1C1的各棱长都是4,E是BC的中点,动点F在线段CA1上,且不与点C、A1重合. 如图所示,四边形ABEF和ABCD都是直角梯形,∠BAD=∠FAB=90°,BC
如图所示,四边形ABEF和ABCD都是直角梯形,∠BAD=∠FAB=90°,BC