题目内容
10.过点(-1,3)且与直线x-2y+3=0平行的直线方程为( )| A. | x-2y+7=0 | B. | 2x+y-1=0 | C. | f(x) | D. | f(5x)>f(3x+4) |
分析 设过点(-1,3)且与直线x-2y+3=0平行的直线方程为 x-2y+m=0,把点(-1,3)代入直线方程,求出m值即得直线l的方程.
解答 解:设过点(-1,3)且与直线x-2y+3=0平行的直线方程为 x-2y+m=0,把点(-1,3)代入直线方程得
-1-2×3+m=0,m=7,故所求的直线方程为x-2y+7=0,
故选A.
点评 本题考查用待定系数法求直线方程的方法,设过点(-1,3)且与直线x-2y+3=0平行的直线方程为x-2y+m=0是解题的关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
1.若a1、b1、c1、a2、b2、c2∈R,且都不为零,则“$\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}$”是“关于x的不等式a1x2+b1x+c1>0与a2x2+b2x+c2>0的解集相同”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
15.对于函数f(x),若在其定义域内存在两个实数a,b(a<b),当x∈[a,b]时,f(x)的值域也是[a,b],则称函数f(x)为“Kobe函数”.若函数f(x)=k+$\sqrt{x-1}$是“Kobe函数”,则实数k的取值范围是( )
| A. | [-1,0] | B. | [1,+∞) | C. | $[{-1,-\frac{3}{4}})$ | D. | $({\frac{3}{4},1}]$ |
20.若关于x的不等式|x-1|+|x-2|>log4a2恒成立,则实数a的取值范围为( )
| A. | (-2,2) | B. | (-∞,-2) | C. | (2,﹢∞) | D. | (-2,0)∪(0,2) |
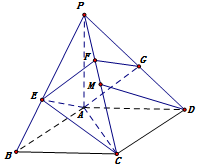 如图,PA垂直于矩形ABCD所在平面,AE⊥PB,垂足为E,EF⊥PC垂足为F.
如图,PA垂直于矩形ABCD所在平面,AE⊥PB,垂足为E,EF⊥PC垂足为F.