题目内容
等腰△ABC的底边
，高CD=3，点E是线段BD上异于点B，D的动点。点F在BC边上，且EF⊥AB。现沿EF将△BEF折起到△PEF的位置，使PE⊥AE，
（Ⅰ）证明EF⊥平面PAE；
（Ⅱ）记BE=x，V（x）表示四棱锥P-ACFE的体积，求V（x）的表达式。
，高CD=3，点E是线段BD上异于点B，D的动点。点F在BC边上，且EF⊥AB。现沿EF将△BEF折起到△PEF的位置，使PE⊥AE， （Ⅰ）证明EF⊥平面PAE；
（Ⅱ）记BE=x，V（x）表示四棱锥P-ACFE的体积，求V（x）的表达式。
解：（Ⅰ）
，
∴
，
故
，
而
，
所以EF⊥平面PAE。
（Ⅱ）
，
∴PE⊥平面ABC，
即PE为四棱锥P-ACFE的高，
由高线CD及EF⊥AB得EF∥CD，
∴
，
由题意知
，∴
，
∴
，
而PE=EB=x，
所以
。
，∴
，故
，而
，所以EF⊥平面PAE。
（Ⅱ）
，∴PE⊥平面ABC，
即PE为四棱锥P-ACFE的高，
由高线CD及EF⊥AB得EF∥CD，
∴
，由题意知
，∴
， ∴
，而PE=EB=x，
所以
。
练习册系列答案
相关题目
如图所示，等腰△ABC的底边AB=6
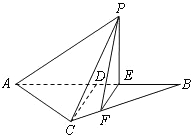如图所示，等腰△ABC的底边
如图，已知等腰△ABC的底边BC=3，顶角为120°，D是BC边上一点，且BD=1．把△ADC沿AD折起，使得平面CAD⊥平面ABD，连接BC形成三棱锥C-ABD．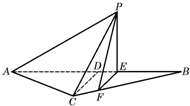
等腰△ABC的底边
（2012•上高县模拟）如图，等腰△ABC的底边AB=6，高CD=3，点E是线段BD上异于点B、D的动点，点F在BC边上，且EF⊥AB．现沿EF将△BEF折起到△PEF的位置，使PE⊥AE，记BE=x，V（x）表示四棱锥P-ACFE的体积．