题目内容
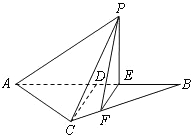 如图所示,等腰△ABC的底边AB=6
如图所示,等腰△ABC的底边AB=6| 6 |
(1)求V(x)的表达式;
(2)当x为何值时,V(x)取得最大值?
(3)当V(x)取得最大值时,求异面直线AC与PF所成角的余弦值.
分析:(1)先求底面面积,再求出高,即可求V(x)的表达式;
(2)利用导数,来求V(x)的最大值,
(3)过F作MF∥AC交AD于M,得到异面直线所成的角,然后求异面直线AC与PF所成角的余弦值.
(2)利用导数,来求V(x)的最大值,
(3)过F作MF∥AC交AD于M,得到异面直线所成的角,然后求异面直线AC与PF所成角的余弦值.
解答:解:(1)由折起的过程可知,PE⊥平面ABC,
S△ABC=9
,S△BEF=
•S△BDC=
x2
V(x)=
x(9-
x2)(0<x<3
)
(2)V′(x)=
(9-
x2),所以x∈(0,6)时,v'(x)>0,V(x)单调递增;
6<x<3
时v'(x)<0,V(x)单调递减;
因此x=6时,V(x)取得最大值12
;
(3)过F作MF∥AC交AD与M,
则
=
=
=
,MB=2BE=12,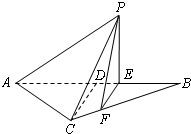
PM=6
,MF=BF=PF=
BC=
=
,
在△PFM中,cos∠PFM=
=
,
∴异面直线AC与PF所成角的余弦值为
.
S△ABC=9
| 6 |
| x2 |
| 54 |
| ||
| 12 |
V(x)=
| ||
| 3 |
| 1 |
| 12 |
| 6 |
(2)V′(x)=
| ||
| 3 |
| 1 |
| 4 |
6<x<3
| 6 |
因此x=6时,V(x)取得最大值12
| 6 |
(3)过F作MF∥AC交AD与M,
则
| BM |
| AB |
| BF |
| BC |
| BE |
| BD |
| BE | ||
|

PM=6
| 2 |
| 6 | ||
3
|
| ||
| 3 |
| 54+9 |
| 42 |
在△PFM中,cos∠PFM=
| 84-72 |
| 84 |
| 1 |
| 7 |
∴异面直线AC与PF所成角的余弦值为
| 1 |
| 7 |
点评:本题考查几何体的体积,导数的应用,异面直线所成的角,考查空间想象能力、逻辑思维能力,是中档题.

练习册系列答案
相关题目
 短长度为
短长度为 如图所示,等腰△ABC的底边AB=6
如图所示,等腰△ABC的底边AB=6 ,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记BE=x,V(x)表示四棱锥P-ACFE的体积.
,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记BE=x,V(x)表示四棱锥P-ACFE的体积.
 ,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记
,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记 ,用
,用 表示四棱锥P-ACFE的体积.
表示四棱锥P-ACFE的体积.