题目内容
8.定义在(0,+∞)上的函数f(x)满足条件:f(xy)=f(x)f(y)对所有正实数x,y成立,且f(2)=4,当x>1时有f(x)>1成立.(Ⅰ)求f(1)和f(8)的值;
(Ⅱ)证明:函数f(x)在(0,+∞)上为单调递增函数;
(Ⅲ)解关于x的不等式:16f($\frac{1}{2x+1}$)≥f(x-3)
分析 (Ⅰ)利用赋值法,代入计算求f(1)和f(8)的值;
(Ⅱ)利用单调性的定义证明函数f(x)在(0,+∞)上为单调递增函数;
(Ⅲ)利用单调性,将不等式化为具体不等式,即可得出结论.
解答 (Ⅰ)解:∵f(xy)=f(x)f(y),∴f(1×2)=f(1)f(2),
∵f(2)=4,∴f(1)=1,
f(4)=f(2)f(2)=16,f(8)=f(2)f(4)=64;
(Ⅱ)证明:设x1>x2>0,则$\frac{{x}_{1}}{{x}_{2}}$>1,
∵当x>1时有f(x)>1成立,
∴f($\frac{{x}_{1}}{{x}_{2}}$)>1,
∴f(x1)=f(x2•$\frac{{x}_{1}}{{x}_{2}}$)=f(x2)f($\frac{{x}_{1}}{{x}_{2}}$)>f(x2)
∴函数f(x)在(0,+∞)上为单调递增函数;
(Ⅲ)解:16f($\frac{1}{2x+1}$)≥f(x-3)可化为f(4×$\frac{1}{2x+1}$)≥f(x-3),
∵函数f(x)在(0,+∞)上为单调递增函数,
∴4×$\frac{1}{2x+1}$≥x-3>0,
∴-1≤x≤$\frac{7}{2}$,
∴不等式的解集为{x|-1≤x≤$\frac{7}{2}$}.
点评 本题考查了抽象函数的应用,考查函数的单调性,考查了数学转化思想方法,是中高档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.使对数loga(一2a+1)有意义的a的取值范围为( )
| A. | a>$\frac{1}{2}$且a≠1 | B. | 0<a<$\frac{1}{2}$ | C. | a>0且a≠1 | D. | a<$\frac{1}{2}$ |
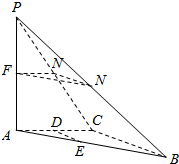 如图,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D、E、F分别为AC、AB、AP的中点,M、N分别为线段PC、PB上的动点,且有MN⊥PC.
如图,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D、E、F分别为AC、AB、AP的中点,M、N分别为线段PC、PB上的动点,且有MN⊥PC.