题目内容
6.在棱长为2的正方体ABCD-A1B1C1D1中,E是棱BB1上的动点,F是棱CD的中点,则四面体A1D1EF体积的最大值是$\frac{4}{3}$.分析 由BB1与平面A1D1F相交可知当E与B1重合时,四面体的体积最大.
解答  解:当E与B1重合时,E到平面A1D1F的距离最大,
解:当E与B1重合时,E到平面A1D1F的距离最大,
即四面体A1D1EF体积取得最大值,
此时V${\;}_{{A}_{1}-{D}_{1}EF}$=V${\;}_{F-{A}_{1}{B}_{1}{D}_{1}}$=$\frac{1}{3}{S}_{△{A}_{1}{B}_{1}{D}_{1}}•A{A}_{1}$=$\frac{1}{3}×\frac{1}{2}×2×2×2$=$\frac{4}{3}$.
故答案为$\frac{4}{3}$.
点评 本题考查了棱锥的体积计算,属于中档题.

练习册系列答案
相关题目
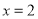 ,则输出的
,则输出的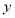 等于( )
等于( )
 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当 时有
时有 .
.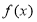 的解析式;
的解析式; 的值域;
的值域;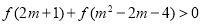 ,求
,求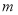 的取值范围.
的取值范围.