题目内容
已知曲线C的极坐标方程 是 =1,以极点为原点,极轴为
=1,以极点为原点,极轴为 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线 的参数方程为
的参数方程为 为参数)。
为参数)。
(1)写出直线 与曲线C的直角坐标方程;
与曲线C的直角坐标方程;
(2)设曲线C经过伸缩变换 得到曲线
得到曲线 ,设曲线
,设曲线 上任一点为
上任一点为 ,求
,求 的最小值。
的最小值。
(1) 
(2) -4
解析试题分析:解:(1)
 (5分)
(5分)
(2) 代入C得
代入C得 (7分)
(7分)
设椭圆的参数方程 为参数) (8分)
为参数) (8分)
则 (10分)
(10分)
则 的最小值为-4。 (12分)
的最小值为-4。 (12分)
考点:参数方程的运用
点评:解决的关键是利用伸缩变换求解析式以及参数方程来得到最值,属于基础题。

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 被直线
被直线 (
( 是参数)截得的弦长.
是参数)截得的弦长. 经过点
经过点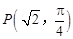 ,圆心为直线
,圆心为直线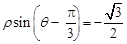 与极轴的交点,求圆
与极轴的交点,求圆 的直线与
的直线与 轴的交点为
轴的交点为 ,与椭圆
,与椭圆  (
( 为参数)交于
为参数)交于 求
求 .
.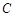 经过点
经过点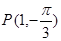 ,圆心为直线
,圆心为直线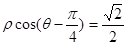 与极轴的交点,求圆
与极轴的交点,求圆 ,过极点的直线
,过极点的直线 (
(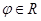 且
且 是参数)交曲线C于两点0,A,令OA的中点为M.
是参数)交曲线C于两点0,A,令OA的中点为M. 时,求M点的直角坐标.
时,求M点的直角坐标. ,圆
,圆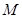 的参数方程为
的参数方程为 (其中
(其中 为参数).
为参数).