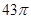题目内容
如图,底面 是边长为2的菱形,且
是边长为2的菱形,且 ,以
,以 与
与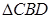 为底面分别作相同的正三棱锥
为底面分别作相同的正三棱锥 与
与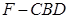 ,且
,且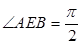 .
.

(1)求证: 平面
平面 ;
;
(2)求多面体 的体积.
的体积.
 是边长为2的菱形,且
是边长为2的菱形,且 ,以
,以 与
与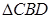 为底面分别作相同的正三棱锥
为底面分别作相同的正三棱锥 与
与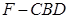 ,且
,且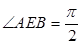 .
.
(1)求证:
 平面
平面 ;
;(2)求多面体
 的体积.
的体积.(1)证明过程见解析;(2) .
.
 .
.试题分析:(1)作
 面
面 于
于 ,作
,作 面
面 于
于 ,易判断四边形
,易判断四边形 是平行四边形,从而有
是平行四边形,从而有 ,又
,又 面
面
 面
面 ,所以
,所以 平面
平面 ;
;(2)取
 的中点
的中点 ,连接
,连接 ,
, ,则多面体
,则多面体 分割成
分割成 ,
, ,
, ,分别求出此三个三棱锥的体积,即可求出多面体
,分别求出此三个三棱锥的体积,即可求出多面体 的体积.
的体积.(1)作
 面
面 于
于 ,作
,作 面
面 于
于 ,
,
因
 与
与 都是正三棱锥,
都是正三棱锥,且
 、
、 分别为
分别为 与
与 的中心,
的中心, 且
且 .
. 所以四边形
 是平行四边形,所以
是平行四边形,所以 .
. 又
 面
面
 面
面 ,所以
,所以 平面
平面 .
. (2)又
 ,则
,则 平面
平面 , 故
, 故 .
. 取
 中点为
中点为 ,联接
,联接 ,即
,即 平面
平面 ,
,易算出


故多面体
 的体积
的体积


练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目

 ,
, ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD 平面BDC(如图乙),设点E,F分别为棱AC,AD的中点.
平面BDC(如图乙),设点E,F分别为棱AC,AD的中点.
 ,求三棱锥A-BFE的体积.
,求三棱锥A-BFE的体积. 的边长为
的边长为 ,点
,点 分别在边
分别在边 上,
上, ,现将△
,现将△ 沿线段
沿线段 折起到△
折起到△ 位置,使得
位置,使得 .
.
 的体积;
的体积; 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 ;若不存在,说明理由.
;若不存在,说明理由. 是母线
是母线 的中点,
的中点, 是底面圆的直径,半径
是底面圆的直径,半径 与母线
与母线 所成的角的大小等于
所成的角的大小等于 .
.
 与
与 所成的角;
所成的角;



 ,E为侧棱PC的中点,则PA与BE所成的角为__________.
,E为侧棱PC的中点,则PA与BE所成的角为__________.
 中,
中, 则四面体外接球的表面积为( )
则四面体外接球的表面积为( )