题目内容
(本小题满分12分)
过椭圆 的右焦点
的右焦点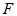 作斜率
作斜率 的直线交椭圆于
的直线交椭圆于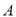 ,
, 两点,且
两点,且 与
与
 共线.
共线.
(Ⅰ)求椭圆的离心率;
(Ⅱ)设 为椭圆上任意一点,且
为椭圆上任意一点,且 . 证明:
. 证明: 为定值.
为定值.
练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
题目内容
(本小题满分12分)
过椭圆 的右焦点
的右焦点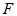 作斜率
作斜率 的直线交椭圆于
的直线交椭圆于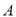 ,
, 两点,且
两点,且 与
与
 共线.
共线.
(Ⅰ)求椭圆的离心率;
(Ⅱ)设 为椭圆上任意一点,且
为椭圆上任意一点,且 . 证明:
. 证明: 为定值.
为定值.
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案