题目内容
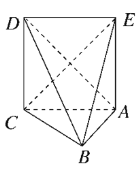
【题目】如图，直三棱柱
的底面是边长为2的正三角形，
，
分别是
，
的中点.
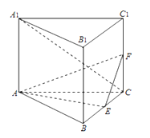
（1）证明：
平面
；
（2）若直线
与平面
所成的角为
，求三棱锥
的体积.
【答案】（1）证明见解析（2）
【解析】
（1）证明AE⊥BB1，AE⊥BC，BC∩BB1＝B，推出AE⊥平面B1BCC1；
（2）取AB的中点G，说明直线A1C与平面A1ABB1所成的角为45°，就是∠CA1G，求出棱锥的高与底面面积即可求解几何体的体积．
（1）证明：∵几何体是直棱柱，∴BB1⊥底面ABC，AE底面ABC，∴AE⊥BB1，
∵直三棱柱ABC﹣A1B1C1的底面是边长为2的正三角形，E分别是BC的中点，
∴AE⊥BC，BC∩BB1＝B，∴AE⊥平面B1BCC1；
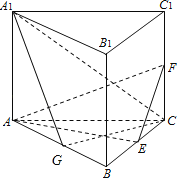
（2）解：取AB的中点G，连结A1G，CG，由（1）可知CG⊥平面A1ABB1，
直线A1C与平面A1ABB1所成的角为45°，就是∠CA1G，则A1G＝CG
，
∴AA1
，CF
．
三棱锥F﹣AEC的体积：
．
练习册系列答案
阅读快车系列答案
相关题目
