题目内容
【题目】已知直线![]() 为椭圆
为椭圆![]() 的右准线,直线
的右准线,直线![]() 与
与![]() 轴的交点记为
轴的交点记为![]() ,过右焦点
,过右焦点![]() 的直线与椭圆交于
的直线与椭圆交于![]() ,
,![]() 两点.
两点.
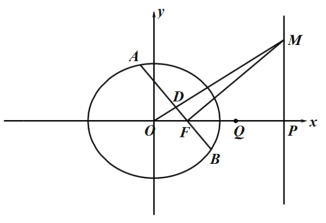
(1)设点![]() 在直线上,且满足
在直线上,且满足![]() ,若直线
,若直线![]() 与线段
与线段![]() 交于点
交于点![]() ,求证:点
,求证:点![]() 为线段
为线段![]() 的中点;
的中点;
(2)设![]() 点的坐标为
点的坐标为![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,试问
,试问![]() 是否为定值,若是,求出这个定值,若不是,请说明理由.
是否为定值,若是,求出这个定值,若不是,请说明理由.
【答案】(1)证明见解析; (2)![]() 为定值0.
为定值0.
【解析】
(1)设直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() , 故直线
, 故直线![]() 的方程为
的方程为![]() .再联立椭圆方程和直线
.再联立椭圆方程和直线![]() ,根据韦达定理求出线段
,根据韦达定理求出线段![]() 的中点为
的中点为![]() ,满足直线
,满足直线![]() 方程
方程![]() ,所以,直线
,所以,直线![]() 与线段
与线段![]() 交点
交点![]() 为线段
为线段![]() 的中点.
的中点.
(2)当直线![]() 的斜率为0时,
的斜率为0时, ![]() . 直线
. 直线![]() 的斜率不为0时,计算直线
的斜率不为0时,计算直线![]() 的方程,求得点
的方程,求得点![]() 的坐标为
的坐标为![]() ,纵坐标与点
,纵坐标与点![]() 相等,即
相等,即![]() ,
,![]() .
.
(1)由椭圆方程为![]() 知,右焦点
知,右焦点![]() 坐标
坐标![]() ,椭圆
,椭圆![]() 的右准线
的右准线![]() 方程为
方程为![]() ,点
,点![]() 坐标
坐标![]() .
.
①当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 与线段
与线段![]() 交点
交点![]() 即为右焦点
即为右焦点![]() ,此时点
,此时点![]() 为线段
为线段![]() 的中点.
的中点.
②又由![]() 知,直线
知,直线![]() 的斜率不为0,故设直线
的斜率不为0,故设直线![]() 的方程为
的方程为![]() ,
,
从而,直线![]() 的方程为
的方程为![]() ,令
,令![]() 得,
得,![]() 点坐标为
点坐标为![]() ,
,
故直线![]() 的方程为
的方程为![]() .
.
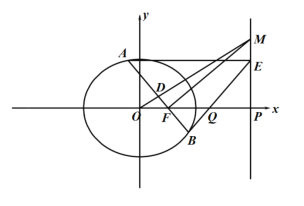
联立方程组 ,消去
,消去![]() 得:
得:![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,
即![]() ,
,![]() ,
,
从而,线段![]() 的中点
的中点![]() .
.
又线段![]() 的中点
的中点![]() 的坐标满足直线
的坐标满足直线![]() 方程
方程![]() ,
,
所以,直线![]() 与线段
与线段![]() 交点
交点![]() 为线段
为线段![]() 的中点.
的中点.
综上可知,点![]() 为线段
为线段![]() 的中点.
的中点.
(2)当直线![]() 的斜率为0时,点
的斜率为0时,点![]() 即为点
即为点![]() ,从而
,从而![]() ,故
,故![]() .
.
直线![]() 的斜率不为0时,
的斜率不为0时,
由(1)知,![]() ,
,![]() ,
,
所以![]() ,则
,则![]() .
.
直线![]() 的方程为
的方程为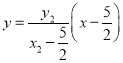 ,又
,又![]() ,
,
令![]() ,得
,得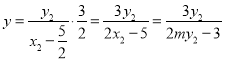
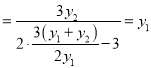 ,
,
所以点![]() 的坐标为
的坐标为![]() ,纵坐标与点
,纵坐标与点![]() 相等。
相等。
即![]() ,所以
,所以![]() .
.
综上可知,![]() 为定值0.
为定值0.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案【题目】大数据时代对于现代人的数据分析能力要求越来越高,数据拟合是一种把现有数据通过数学方法来代入某条数式的表示方式,比如![]() ,
,![]()
![]() ,2,
,2,![]() ,n是平面直角坐标系上的一系列点,用函数
,n是平面直角坐标系上的一系列点,用函数![]() 来拟合该组数据,尽可能使得函数图象与点列
来拟合该组数据,尽可能使得函数图象与点列![]() 比较接近.其中一种描述接近程度的指标是函数的拟合误差,拟合误差越小越好,定义函数
比较接近.其中一种描述接近程度的指标是函数的拟合误差,拟合误差越小越好,定义函数![]() 的拟合误差为:
的拟合误差为:![]() .已知平面直角坐标系上5个点的坐标数据如表:
.已知平面直角坐标系上5个点的坐标数据如表:
x | 1 | 3 | 5 | 7 | 9 |
y | 12 |
| 4 |
| 12 |
![]() 若用一次函数
若用一次函数![]() 来拟合上述表格中的数据,求该函数的拟合误差
来拟合上述表格中的数据,求该函数的拟合误差![]() 的最小值,并求出此时的函数解析式
的最小值,并求出此时的函数解析式![]() ;
;
![]() 若用二次函数
若用二次函数![]() 来拟合题干表格中的数据,求
来拟合题干表格中的数据,求![]() ;
;
![]() 请比较第
请比较第![]() 问中的
问中的![]() 和第
和第![]() 问中的
问中的![]() ,用哪一个函数拟合题目中给出的数据更好?
,用哪一个函数拟合题目中给出的数据更好?![]() 请至少写出三条理由
请至少写出三条理由![]()