题目内容
已知抛物线y=-
x2,过点M(0,-1)的直线l与抛物线交于A,B两点,若直线OA,OB的斜率之和为1,求直线l的方程.
| 1 |
| 2 |
考点:直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:由题意可得设直线l的方程为y=kx-1,联立直线与抛物线的方程可得:x2+2kx-2=0,根据韦达定理可得答案.
解答:
解:由题意可得直线l的斜率存在,设直线l的方程为y=kx-1,A(x1,y1),B(x2,y2),
所以联立直线与抛物线的方程可得:x2+2kx-2=0,
所以x1+x2=-2k,x1x2=-2,
因为OA和OB的斜率之和为1,即
+
=1,
所以
+
=2k-
=1,
所以k=1,
所以直线l的方程为y=x-1.
所以联立直线与抛物线的方程可得:x2+2kx-2=0,
所以x1+x2=-2k,x1x2=-2,
因为OA和OB的斜率之和为1,即
| y1 |
| x1 |
| y2 |
| x2 |
所以
| kx1-1 |
| x1 |
| kx2-1 |
| x2 |
| x1+x2 |
| x1x2 |
所以k=1,
所以直线l的方程为y=x-1.
点评:本题主要考查抛物线的简单性质、直线的一般式方程、直线与抛物线的位置关系,以及方程思想,属于中档题.

练习册系列答案
相关题目
已知ξ的分布列为:
则Dξ等于( )
| ξ | 1 | 2 | 3 | 4 | ||||||||
| P |
|
|
|
|
A、
| ||
B、
| ||
C、
| ||
D、
|
下列说法中正确的是( )
①f(x)=x0与g(x)=1是同一个函数;
②y=f(x)与y=f(x+1)有可能是同一个函数;
③y=f(x)与y=f(t)是同一个函数;
④定义域和值域相同的函数是同一个函数.
①f(x)=x0与g(x)=1是同一个函数;
②y=f(x)与y=f(x+1)有可能是同一个函数;
③y=f(x)与y=f(t)是同一个函数;
④定义域和值域相同的函数是同一个函数.
| A、①② | B、②③ | C、②④ | D、①③ |
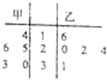 将甲、乙两名篮球运动员在篮球比赛中的得分制成茎叶图如图所示,若
将甲、乙两名篮球运动员在篮球比赛中的得分制成茎叶图如图所示,若. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
用辗转相除法,计算56和264的最大公约数时,需要做的除法次数是( )
| A、3 | B、4 | C、6 | D、7 |
