题目内容
已知定义域为 的函数
的函数 同时满足以下三个条件:
同时满足以下三个条件:
(1) 对任意的 ,总有
,总有 ;(2)
;(2) ;(3) 若
;(3) 若 ,
, ,且
,且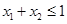 ,则有
,则有 成立,则称
成立,则称 为“友谊函数”,请解答下列各题:
为“友谊函数”,请解答下列各题:
(1)若已知 为“友谊函数”,求
为“友谊函数”,求 的值;
的值;
(2)函数 在区间
在区间 上是否为“友谊函数”?并给出理由.
上是否为“友谊函数”?并给出理由.
(3)已知 为“友谊函数”,假定存在
为“友谊函数”,假定存在 ,使得
,使得 且
且 , 求证:
, 求证: .
.
(1)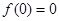 (2)是友谊函数(3)见解析.
(2)是友谊函数(3)见解析.
解析试题分析:(1)利用赋值法由 得
得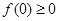 ,再由
,再由 得
得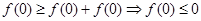 ,所以
,所以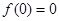 (2)分别验证(1)由指数函数的性质
(2)分别验证(1)由指数函数的性质 在区间
在区间 上的最小值为0,(2)直接带入验证易得
上的最小值为0,(2)直接带入验证易得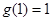 (3)利用做差法直接比较
(3)利用做差法直接比较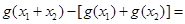
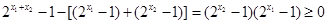 (3) 先利用单调性的定义证明抽象函数的单调性,然后再证明
(3) 先利用单调性的定义证明抽象函数的单调性,然后再证明
取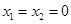 得
得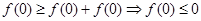 , 又由
, 又由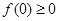 ,
,
得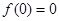
(2)显然 在
在 上满足(1)
上满足(1) 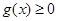 ;(2)
;(2)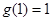 .(3)若
.(3)若 ,
, ,且
,且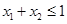 ,则有
,则有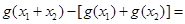
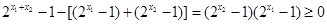
故 满足条件(1)、(2)、(3),所以
满足条件(1)、(2)、(3),所以 为友谊函数.
为友谊函数.
(3)由 (3)知任给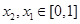 其中
其中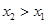 ,且有
,且有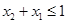 ,不妨设
,不妨设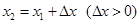

所以: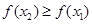 .
.
下面证明 :(i)若
:(i)若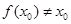 ,则有
,则有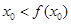 或
或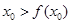
若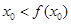 ,则
,则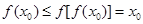 ,这与
,这与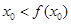 矛盾;
矛盾;
(2)若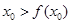 ,则
,则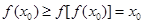 ,这与
,这与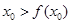 矛盾;
矛盾;
综上所述:
考点:函数的概念与性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
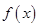 是定义在
是定义在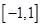 上的奇函数,在
上的奇函数,在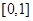 上
上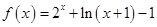 .
.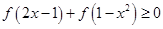 .
.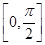 上恒成立.
上恒成立.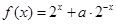
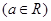 .
.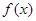 的奇偶性;
的奇偶性;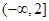 上为减函数,求
上为减函数,求 的取值范围.
的取值范围.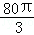 立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>3)千元.设该容器的建造费用为y千元.
立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>3)千元.设该容器的建造费用为y千元.
 a为常数且a>0.
a为常数且a>0. 对称;
对称;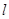 (宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数
(宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数 )的图象,且点M到边OA距离为
)的图象,且点M到边OA距离为 .
.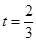 时,求直路
时,求直路
 的定义域为E,值域为F.
的定义域为E,值域为F.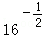 与集合F的关系;
与集合F的关系;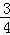 },求实数a的值.
},求实数a的值.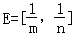 ,F=[2﹣3m,2﹣3n],求m,n的值.
,F=[2﹣3m,2﹣3n],求m,n的值.