题目内容
函数y=2sin（
），x∈[
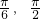]的值域为________．
[-2，-1]
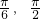分析：根据已知中函数y=2sin（），x∈[]的解析式和定义域，先求出的取值范围，再根据正弦型函数的性质，得到函数的最大值和最小值，进而得到函数的值域．
解答：当x∈[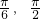]时，∈[-
，-
]
当=-或-时，即x=或
时，函数y=2sin（）取最大值-1；
当=-时，x=
时，函数y=2sin（）取最小值-2；
则函数y=2sin（）的值域为[-2，-1]
故答案为：[-2，-1]
点评：本题考查的知识点是正弦函数的定义域和值域，其中熟练掌握正弦型函数的性质，是解答本题的关键，属于基础题．
分析：根据已知中函数y=2sin（
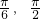），x∈[]的解析式和定义域，先求出的取值范围，再根据正弦型函数的性质，得到函数的最大值和最小值，进而得到函数的值域．解答：当x∈[
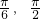]时，∈[-，-]当
=-或-时，即x=或时，函数y=2sin（）取最大值-1；当
=-时，x=时，函数y=2sin（）取最小值-2；则函数y=2sin（
）的值域为[-2，-1]故答案为：[-2，-1]
点评：本题考查的知识点是正弦函数的定义域和值域，其中熟练掌握正弦型函数的性质，是解答本题的关键，属于基础题．
练习册系列答案
天天向上口算本系列答案
相关题目
如图所示，点P是函数y=2sin（ωx+φ）（x∈R，ω＞0）图象的最高点，M、N是图象与x轴的交点，若函数y=2sin(2x-
)的图象（ ）
| π |
| 6 |
| A、关于原点成中心对称 | ||
| B、关于y轴成轴对称 | ||
C、关于(
| ||
D、关于直线x=
|