题目内容
已知m∈R,命题p:对于任意x∈[0,8],不等式log
(x+1)≥m2-3恒成立;命题q:对任意x∈R,不等式|1+sin2x-cos2x|≤2m|cos(x-
)|恒成立.
(1)若p为真命题,求m的取值范围;
(2)若p且q为假,p或q为真,求m的取值范围.
| 1 |
| 3 |
| π |
| 4 |
(1)若p为真命题,求m的取值范围;
(2)若p且q为假,p或q为真,求m的取值范围.
考点:复合命题的真假
专题:简易逻辑
分析:先将命题p,q为真时的m的范围为求出来,然后再进一步求解即可.
解答:
解:(1)对于任意x∈[0,8],不等式log
(x+1)≥m2-3恒成立,
令f(x)=log
(x+1),x∈[0,8].显然该函数是减函数,所以f(x)min=f(8)=-2.
所以要使原式成立,只需m2-3≤-2,即m2-3+2≤0,解得1≤m≤2.
(2)对于q,因为1+sin2x-cos2x=2sinxcosx+2sin2x=2sinx(cosx+sinx)=2sinx•
cos(x-
).
当cos(x-
)=0时,原式显然成立.
当cos(x-
)≠0时,原式可化为m≥
|sinx|.
要使原式恒成立,只需m≥
即可.
因为“p且q为假,p或q为真”,故p,q一真一假,
所以
或
,解得m>2或1≤m<
.
| 1 |
| 3 |
令f(x)=log
| 1 |
| 3 |
所以要使原式成立,只需m2-3≤-2,即m2-3+2≤0,解得1≤m≤2.
(2)对于q,因为1+sin2x-cos2x=2sinxcosx+2sin2x=2sinx(cosx+sinx)=2sinx•
| 2 |
| π |
| 4 |
当cos(x-
| π |
| 4 |
当cos(x-
| π |
| 4 |
| 2 |
要使原式恒成立,只需m≥
| 2 |
因为“p且q为假,p或q为真”,故p,q一真一假,
所以
|
|
| 2 |
点评:本题考查了复合命题真假的判断方法,要注意“或命题”“且命题”的区别与联系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
为了了解高一学生的身体发育情况,打算在高一年级10个班中某两个班按男女生比例抽取样本,正确的是( )
| A、随机抽样 |
| B、分层抽样 |
| C、先用分层抽样,再用随机数表法 |
| D、先用抽签法,再用分层抽样 |
△ABC中,∠A、∠B、∠C对应边分别是a、b、c,则两直线l1:xsinA+ay+c=0,l2:bx-ysinB+sinC=0则l1与l2位置关系是( )
| A、平行 | B、重合 |
| C、垂直 | D、相交不垂直 |
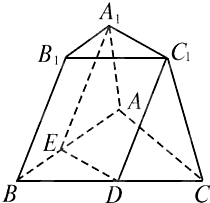 如图所示,在两个底面对应边的比是1:2的三棱台ABC-A1B1C1中,BB1∥截面A1EDC1,求截面A1EDC1截棱台ABC-A1B1C1成两部分体积之比.
如图所示,在两个底面对应边的比是1:2的三棱台ABC-A1B1C1中,BB1∥截面A1EDC1,求截面A1EDC1截棱台ABC-A1B1C1成两部分体积之比.