题目内容
11.计算:(1)2log210+log20.04
(2)(log43+log83)•(log35+log95)•(log52+log252)
分析 (1)(2)利用对数的运算性质即可得出.
解答 解:(1)原式=$lo{g}_{2}(1{0}^{2}×0.04)$=$lo{g}_{2}{2}^{2}$=2.
(2)原式=$(\frac{lg3}{2lg2}+\frac{lg3}{3lg2})$×$(\frac{lg5}{lg3}+\frac{lg5}{2lg3})$×$(\frac{lg2}{lg5}+\frac{lg2}{2lg5})$
=$\frac{lg3}{lg2}×\frac{lg5}{lg3}×\frac{lg2}{lg5}$×$(\frac{1}{2}+\frac{1}{3})$×$(1+\frac{1}{2})$×$(1+\frac{1}{2})$
=$\frac{15}{8}$.
点评 本题考查了对数的运算性质、换底公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.随机变量X的概率分布列如下表如示,且$P(X=n)=\left\{\begin{array}{l}\frac{7}{10},n=1\\ \frac{1}{n(n+1)},n≥2且n∈z\end{array}\right.$,
(Ⅰ)由分布列的性质试求n的值,并求随机变量X的分布列与数学期望;
(Ⅱ)一个盒子里装有标号为1,2,…,n且质地相同的标签若干张,从中任取1张标签所得的标号为随机变量X.现有放回的从中每次抽取一张,共抽取三次,求恰好2次取得标签的标号不小于3的概率.
| X | X1 | X2 | X3 | … | Xn |
| P | p1 | p2 | p3 | … | pn |
(Ⅱ)一个盒子里装有标号为1,2,…,n且质地相同的标签若干张,从中任取1张标签所得的标号为随机变量X.现有放回的从中每次抽取一张,共抽取三次,求恰好2次取得标签的标号不小于3的概率.
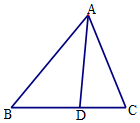 在△ABC中,角A,B,C所对的边分别为a,b,c,已知${S_{△ABC}}=\frac{{\sqrt{3}}}{2}accosB$,
在△ABC中,角A,B,C所对的边分别为a,b,c,已知${S_{△ABC}}=\frac{{\sqrt{3}}}{2}accosB$,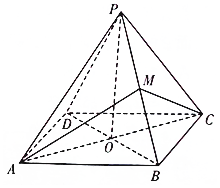 四棱锥P-ABCD的四条侧棱长相等,底面ABCD为正方形,M为PB的中点.
四棱锥P-ABCD的四条侧棱长相等,底面ABCD为正方形,M为PB的中点.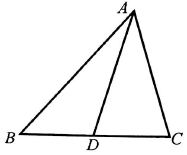 已知a,b,c分别为△ABC三个内角A,B,C的对边,且acosC+$\sqrt{3}$asinC-b-c=0.
已知a,b,c分别为△ABC三个内角A,B,C的对边,且acosC+$\sqrt{3}$asinC-b-c=0.