题目内容
已知函数f(x)=(log2x)2+4log2x+m,x∈[
,4],m为常数.
(Ⅰ)设函数f(x)存在大于1的零点,求实数m的取值范围;
(Ⅱ)设函数f(x)有两个互异的零点α,β,求m的取值范围,并求α•β的值.
| 1 |
| 8 |
(Ⅰ)设函数f(x)存在大于1的零点,求实数m的取值范围;
(Ⅱ)设函数f(x)有两个互异的零点α,β,求m的取值范围,并求α•β的值.
考点:二次函数在闭区间上的最值
专题:函数的性质及应用
分析:(Ⅰ)转化g(t)=t2+4t+m,t∈[-3,2]g(t)在t∈(0,2]时有零点g(t)表示的二次函数开口向上,对称轴为t0=-2,根据二次函数求解得出即
⇒
即可.
(Ⅱ)根据二次函数得出
⇒
⇒3≤m<4,运用韦达定理求解即可,方程g(t)=t2+4t+m=0的两根t1+t2=-4,即再运用对数求解即可,log2α+log2β=-4⇒log2αβ=-4⇒αβ=
,
|
|
(Ⅱ)根据二次函数得出
|
|
| 1 |
| 16 |
解答:
解:(Ⅰ)函数f(x)=(log2x)2+4log2x+m,x∈[
,4],m为常数.
令t=log2x,
∵x∈[
,4],∴t∈[-3,2]
则 由已知,若f(x)存在大于1的零点,即g(t)在t∈(0,2]时有零点g(t)表示的二次函数开口向上,对称轴为t0=-2,
所以若g(t)在t∈(0,2]时有零点,即
⇒
⇒-12≤m<0
即m的取值范围为[-12,0,
(Ⅱ)若f(x)有两个相异的零点,
即g(t)在t∈[-3,2]
时有两个相异零点
∴g(t)表示的二次函数开口向上,对称轴为t0=-2
∴
⇒
⇒3≤m<4
即m的取值范围为[3,4),
此时,方程g(t)=t2+4t+m=0的两根t1+t2=-4
即log2α+log2β=-4⇒log2αβ=-4⇒αβ=
,
| 1 |
| 8 |
令t=log2x,
∵x∈[
| 1 |
| 8 |
则 由已知,若f(x)存在大于1的零点,即g(t)在t∈(0,2]时有零点g(t)表示的二次函数开口向上,对称轴为t0=-2,
所以若g(t)在t∈(0,2]时有零点,即
|
|
即m的取值范围为[-12,0,
(Ⅱ)若f(x)有两个相异的零点,
即g(t)在t∈[-3,2]
时有两个相异零点
∴g(t)表示的二次函数开口向上,对称轴为t0=-2
∴
|
|
即m的取值范围为[3,4),
此时,方程g(t)=t2+4t+m=0的两根t1+t2=-4
即log2α+log2β=-4⇒log2αβ=-4⇒αβ=
| 1 |
| 16 |
点评:本题综合考查了函数的性质,不等式,方程,函数的零点的求解,属于中档题,关键是确定相应的函数解析式,以及范围.

练习册系列答案
相关题目
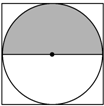 在如图所示的正方形中随机掷一粒豆子,豆子落在正方形内切圆的上半圆(圆中阴影部分)中的概率是
在如图所示的正方形中随机掷一粒豆子,豆子落在正方形内切圆的上半圆(圆中阴影部分)中的概率是