题目内容
11.在正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1、AD的中点.那么异面直线OE和FD1所成角的余弦值为$\frac{\sqrt{15}}{5}$.分析 建立空间直角坐标系,利用向量的夹角公式即可得出异面直线所成的夹角.
解答  解:如图所示
解:如图所示
不妨设AB=2,
则D(0,0,0),A(2,0,0),B(2,2,0),C(0,2,0),
C1(0,2,2),D1(0,0,2),O(1,1,0),E(0,2,1),F(1,0,0).
∴$\overrightarrow{OE}$=(-1,1,1),$\overrightarrow{F{D}_{1}}$=(-1,0,2).
∴$cos<\overrightarrow{OE},\overrightarrow{F{D}_{1}}>$=$\frac{\overrightarrow{OE}•\overrightarrow{F{D}_{1}}}{|\overrightarrow{OE}||\overrightarrow{F{D}_{1}}|}$=$\frac{1+2}{\sqrt{3}×\sqrt{5}}$=$\frac{\sqrt{15}}{5}$.
∴异面直线OE和FD1所成角的余弦值为$\frac{\sqrt{15}}{5}$.
故答案为:$\frac{\sqrt{15}}{5}$.
点评 本题考查了利用向量的夹角公式求异面直线所成的夹角,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
20.程序框图如图所示:如果输入x=5,则输出结果为( )


| A. | 325 | B. | 109 | C. | 973 | D. | 295 |
1.圆心在曲线y=$\frac{1}{x}$(x>0)上,与直线2x+y+1=0相切且面积最小的圆的方程为( )
| A. | (x-1)2+(y-2)2=5 | B. | (x-1)2+(y-1)2=5 | C. | (x-1)2+(y-2)2=25 | D. | (x-1)2+(y-1)2=25 |
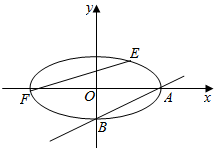 已知椭圆线$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,如图所示,A(a,0),B(0,-b)原点到直线AB的距离为$\frac{4}{\sqrt{5}}$.
已知椭圆线$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,如图所示,A(a,0),B(0,-b)原点到直线AB的距离为$\frac{4}{\sqrt{5}}$.